题目内容
若tanα=3，tanβ=5，则tan（α-β）的值为（ ）
A、-
| ||
B、-
| ||
C、
| ||
D、-
|
考点：两角和与差的正切函数
专题：三角函数的求值
分析：由条件利用两角差的正切公式求得tan（α-β）的值．
解答：
解：tanα=3，tanβ=5，则tan（α-β）=
=
=-
，
故选：A．
| tanα-tanβ |
| 1+tanαtanβ |
| 3-5 |
| 1+3×5 |
| 1 |
| 8 |
故选：A．
点评：本题主要考查两角差的正切公式的应用，属于基础题．
练习册系列答案
相关题目
已知 tanα＞0，cosα＜0，则角α的终边在第（ ）象限．
| A、一 | B、二 | C、三 | D、四 |
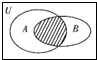设全集U=R，A={x∈Z|-2≤x≤2}，B={x∈R|x2+3x＜0}，则如图中阴影部分表示的集合为（ ）| A、{-1} |
| B、{-2，-1} |
| C、{-2，-1，0} |
| D、（-2，-1） |
在等差数列{an}中，a1=1，a4=7，则公差d为（ ）
| A、4 | B、6 | C、1 | D、2 |
若x∈[0，
]，则使等式cos（πcosx）=0成立的x的值是（ ）
| 3π |
| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
如图，是某算法流程图的一部分，其算法的逻辑结构为（ ）
| A、顺序结构 | B、条件结构 |
| C、判断结构 | D、循环结构 |
已知函数f（x）=x3+ax2+b的图象在点P （1，0）处的切线与直线3x+y=0平行．则a、b的值分别为（ ）
| A、-3，2 | B、-3，0 |
| C、3，2 | D、3，-4 |
若A（x，1-x，2x），B（1，-2，x-1），当|
|取最小值时，x的值等于（ ）
| AB |
| A、1 | B、0 | C、-2 | D、-1 |
函数f（x）=
的定义域是（ ）
| ||
| x |
| A、（0，+∞） |
| B、（-1，0）∪（0，+∞） |
| C、[-1，0）∪（0，+∞） |
| D、（0，1） |