题目内容
18.函数f(x)=$\frac{1}{2}{x^2}$-2lnx的单调递减区间是(0,$\sqrt{2}$).分析 求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可.
解答 解:f(x)=$\frac{1}{2}{x^2}$-2lnx的定义域是(0,+∞),
f′(x)=x-$\frac{2}{x}$=$\frac{{x}^{2}-2}{x}$,
令f′(x)<0,解得:0<x<$\sqrt{2}$,
故函数f(x)=$\frac{1}{2}{x^2}$-2lnx的单调递减区间是(0,$\sqrt{2}$),
故答案为:(0,$\sqrt{2}$).
点评 本题考查了函数的单调性问题,考查导数的应用,是一道基础题.

练习册系列答案
相关题目
9.已知等差数列{an}的前n项和记为Sn,若a4+a6+a8=15,则S11的值为( )
| A. | 55 | B. | $\frac{55}{2}$ | C. | 165 | D. | $\frac{165}{2}$ |
13.函数f(x)=lnx+1的定义域为( )
| A. | (0,+∞) | B. | (1,+∞) | C. | (-1,+∞) | D. | R |
10.将点P的直角坐标(-$\sqrt{3}$,-1)化成极坐标( )
| A. | (2,$\frac{π}{3}$) | B. | (2,$\frac{π}{2}$) | C. | (2,$\frac{4π}{3}$) | D. | (2,$\frac{7π}{6}$) |
8.如图是-个几何体的三视图,在该几何体的各个面中,面积最小的面的面积为( )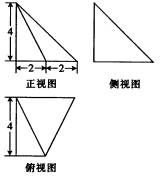

| A. | 4 | B. | 8 | C. | 4$\sqrt{3}$ | D. | 4$\sqrt{2}$ |