题目内容
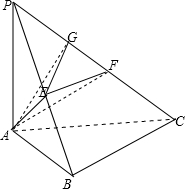
已知PA⊥△ABC所在的平面,∠ABC=90°,E、F分别是PB、PC上的点,且AE⊥PB.
(1)求证:平面AEF⊥平面PBC;
(2)若AB=4,BC=3,PA=2,求二面角A-PC-B的大小.
(1)求证:平面AEF⊥平面PBC;
(2)若AB=4,BC=3,PA=2,求二面角A-PC-B的大小.
考点:二面角的平面角及求法,平面与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)首先利用线面垂直得到,线线垂直,进一步利用线线垂直转化出线面垂直,再得到面面相垂直.
(2)利用第一步的结论AE⊥平面PBC,AE⊥PC,过E做EG⊥PC,连接AG.则:PC⊥平面AEG,所以∠AGE就是二面角A-PC-B的平面角.在△APB中,AB=4,BC=3,PA=2,利用面积相等:PA•AB=PB•AE解得:AE=
在△PAC中,利用面积相等:AC•PA=PC•AF,解得:AF=
,最后解得:sin∠AGE=
=
(2)利用第一步的结论AE⊥平面PBC,AE⊥PC,过E做EG⊥PC,连接AG.则:PC⊥平面AEG,所以∠AGE就是二面角A-PC-B的平面角.在△APB中,AB=4,BC=3,PA=2,利用面积相等:PA•AB=PB•AE解得:AE=
4
| ||
| 5 |
10
| ||
| 29 |
| AE |
| AG |
2
| ||
| 25 |
解答:
证明:(1)PA⊥△ABC所在的平面,
所以:PA⊥BC
∵∠ABC=90°,
∴BC⊥AB
∴BC⊥平面PAB
AE?平面PAB
BC⊥AE
∵E、F分别是PB、PC上的点,
且AE⊥PB.
∴AE⊥平面PBC
AE?平面AEF
∴平面AEF⊥平面PBC
解:(2)利用(1)的结论AE⊥平面PBC
∴AE⊥PC
过E做EG⊥PC,连接AG
则:PC⊥平面AEG
所以∠AGE就是二面角A-PC-B的平面角.
在△APB中,AB=4,BC=3,PA=2,
利用面积相等:PA•AB=PB•AE
解得:AE=
在△PAC中,利用面积相等:AC•PA=PC•AF
解得:AF=
sin∠AGE=
=
故二面角A-PC-B的平面角为arcsin
.
所以:PA⊥BC
∵∠ABC=90°,
∴BC⊥AB
∴BC⊥平面PAB
AE?平面PAB
BC⊥AE
∵E、F分别是PB、PC上的点,
且AE⊥PB.
∴AE⊥平面PBC
AE?平面AEF
∴平面AEF⊥平面PBC
解:(2)利用(1)的结论AE⊥平面PBC
∴AE⊥PC
过E做EG⊥PC,连接AG
则:PC⊥平面AEG
所以∠AGE就是二面角A-PC-B的平面角.
在△APB中,AB=4,BC=3,PA=2,
利用面积相等:PA•AB=PB•AE
解得:AE=
4
| ||
| 5 |
在△PAC中,利用面积相等:AC•PA=PC•AF
解得:AF=
10
| ||
| 29 |
sin∠AGE=
| AE |
| AG |
2
| ||
| 25 |
故二面角A-PC-B的平面角为arcsin
2
| ||
| 25 |

点评:本题考查的知识要点:线面垂直的判定和性质定理,面面垂直的判定定理,勾股定理的应用,二面角平面角的做法,及相关的运算问题.属于基础题型.

练习册系列答案
相关题目
设动点A、B均在双曲线C:
-
=1(a>0,b>0)的右支上,点O为坐标原点,双曲线C的离心率为e,则( )
| x2 |
| a2 |
| y2 |
| b2 |
A、若e>
| ||||||
B、若1≤e≤
| ||||||
C、若e>
| ||||||
D、若1<e≤
|
已知函数f(x)=
则方程f(x)=1解的个数为( )
|
| A、1 | B、2 | C、3 | D、4 |
