题目内容
4.已知f(x)为一元二次函数,且m,f(m),f(f(m)),f(f(f(m)))成正项等比数列,求证:f(m)=m.分析 可以设t=f(f(m)),f(t)=f(f(f(m))),由m,f(m),t,f(t)成等比数列,就有mf(t)=tf(m),可以发现式子有对称性,不妨转换成$\frac{f(t)}{f(m)}$=$\frac{t}{m}$,可设g(x)=$\frac{f(f(x))}{x}$,由二次函数f(x),可得g(x)为单调函数,即有f(m)=m.
解答 证明:要证明f(m)=m,就必须列出等式,没有等式就构造等式.
为了简便易懂,可以设t=f(f(m)),f(t)=f(f(f(m))),
显然就要构造出等式m=t就能证出要证的结论,
由m,f(m),t,f(t)成等比数列,就有mf(t)=tf(m),可以发现式子有对称性,
不妨转换成$\frac{f(t)}{f(m)}$=$\frac{t}{m}$,
我们就可以构造函数g(x)=$\frac{f(f(x))}{x}$,
上式就等价于g(f(m))=g(m),
因为f(x)是二次函数,可以很容易的知道g(x)在其指定区间内是单调函数,
有f(m)=m.
点评 本题考查等式的证明,考查等比数列的性质的运用,注意运用对称性和构造函数法,考查推理能力,属于难题.

练习册系列答案
相关题目
14.执行如图的程序框图,如果输入的N=10,则输出的x=( )
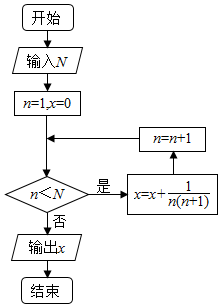

| A. | 0.5 | B. | 0.8 | C. | 0.9 | D. | 1 |
12.已知i是虚数单位,若复数z满足z=$\frac{{i}^{3}}{1+i}$,则z的共轭复数$\overline{z}$为( )
| A. | $\frac{1+i}{2}$ | B. | $\frac{1-i}{2}$ | C. | $\frac{-1+i}{2}$ | D. | $\frac{-1-i}{2}$ |
16.将向量$\overrightarrow{a_1}$=(x1,y1),$\overrightarrow{a_2}$=(x2,y2),…$\overrightarrow{a_n}$=(xn,yn)组成的系列称为向量列{$\overrightarrow{a_n}$},并定义向量列{$\overrightarrow{a_n}$}的前n项和$\overrightarrow{S_n}=\overrightarrow{a_1}+\overrightarrow{a_2}+…+\overrightarrow{a_n}$.如果一个向量列从第二项起,每一项与前一项的差都等于同一个向量,那么称这样的向量列为等差向量列.若向量列{$\overrightarrow{a_n}$}是等差向量列,那么下述四个向量中,与$\overrightarrow{{S_{21}}}$一定平行的向量是( )
| A. | $\overrightarrow{{a_{10}}}$ | B. | $\overrightarrow{{a_{11}}}$ | C. | $\overrightarrow{{a_{20}}}$ | D. | $\overrightarrow{{a_{21}}}$ |
13.下列函数中,既是偶函数又在区间(0,+∞)上单调递减的是( )
| A. | y=x3 | B. | y=e-x | C. | y=-x2+1 | D. | y=lg|x| |
 如图,在边长分别为f(x)与g(x)和2π的矩形内有由函数y=sinx的图象和x轴围成的区域(阴影部分),李明同学用随机模拟的方法估算该区域的面积.若在矩形内每次随机产生9000个点,并记录落在该区域内的点的个数.经过多次试验,计算出落在该区域内点的个数平均值为3000个,若π的近似值为3,则该区域的面积约为( )
如图,在边长分别为f(x)与g(x)和2π的矩形内有由函数y=sinx的图象和x轴围成的区域(阴影部分),李明同学用随机模拟的方法估算该区域的面积.若在矩形内每次随机产生9000个点,并记录落在该区域内的点的个数.经过多次试验,计算出落在该区域内点的个数平均值为3000个,若π的近似值为3,则该区域的面积约为( )