题目内容
15.已知数列{an}满足an+2=an+1+an(n∈N*),a1=a2=1,把数列各项依次除以3所得的余数记为数列{bn},除以4所得的余数记为数列{cn},则b2016+c2016=0.分析 {an}是斐波那契数列,求得{an}中各项除以3所得余数组成以8为周期的周期数列,各项除以4所得余数组成以6为周期的周期数列,从而可得结论.
解答 解:依题意,该数列为:1,1,2,3,5,8,13,21,34,55,89,144,…
各项依次除以3所得的余数记为数列{bn},则为1,1,2,0,2,2,1,0,1,1,2,0,…,即{cn}中各项除以3所得余数组成以8为周期的周期数列,
而2016=252×8,故b2016=0
除以4所得的余数记为数列{cn},则1,1,2,3,1,0,1,1,2,3,1,0,…即{cn}中各项除以4所得余数组成以6为周期的周期数列,
而2016=336×6,故C2016=0,
故b2016+c2016=0,
故答案为:0.
点评 本题考查了斐波那契数列,以及周期数列,考查了学生的分析问题解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.执行如图的程序框图(n∈N*),则输出的S=( )
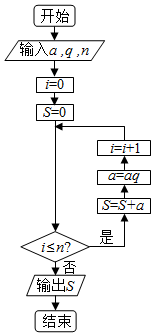

| A. | a+aq+…+aqn-1 | B. | $\frac{{a(1-{q^n})}}{1-q}$ | C. | a+aq+…+aqn | D. | $\frac{{a(1-{q^{n+1}})}}{1-q}$ |
6.执行如图所示的程序框图,若输出的n=7,则输入的整数K的最大值是( )


| A. | 18 | B. | 50 | C. | 78 | D. | 306 |
20.设P(x,y)满足$\left\{\begin{array}{l}{x≥1}\\{y≥1}\\{x+y≤4}\end{array}\right.$,点A(2,0),B(0,3),若$\overrightarrow{OP}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$,O是坐标原点,则λ+μ的取值范围是( )
| A. | [2,4] | B. | [$\frac{5}{6}$,$\frac{11}{6}$] | C. | [$\frac{5}{6}$,2] | D. | [1,2] |
5.已知变量x、y满足的不等式组$\left\{\begin{array}{l}x≥0\\ 2x-y≤0\\ kx-y+1≥0\end{array}\right.$表示的平面区域是一个直角三角形,则实数k=( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 0 | D. | 0或-$\frac{1}{2}$ |