题目内容
5.从[0,2]中任取一个数x,从[0,3]中任取一个数y,则使x2+y2≤4的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{π}{9}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
分析 在平面直角坐标系中作出图形,则x∈[0,2],y∈[0,3]的平面区域为矩形,符合条件x2+y2≤4的区域为以原点为圆心,2为半径的扇形内部,则扇形面积与矩形面积的比为概率
解答 解:在平面直角坐标系中作出图形,如图所示,
则x∈[0,2],y∈[0,3]的平面区域为矩形OABC,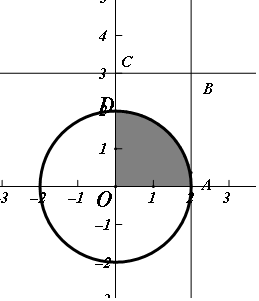
符合条件x2+y2≤4的区域为以原点为圆心,
2为半径的扇形OAD内部,
∴P(x2+y2≤4)=$\frac{{S}_{扇形}}{{S}_{矩形}}$=$\frac{\frac{1}{4}π×{2}^{2}}{2×3}$=$\frac{π}{6}$;
故选D.
点评 本题考查了几何概型的概率计算,正确作出几何图形是解题的关键.

练习册系列答案
相关题目
10.已知关于x的不等式x2-4ax+3a2<0(a>0)的解集为(x1,x2),则${x_1}+{x_2}+\frac{a}{{{x_1}{x_2}}}$的最小值是( )
| A. | $\frac{{\sqrt{6}}}{3}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $\frac{{4\sqrt{3}}}{3}$ | D. | $-\frac{{4\sqrt{3}}}{3}$ |
10.函数y=ln(ex-x+a)(e为自然对数的底数)的值域是正实数集R+,则实数a的取值范围是( )
| A. | (-∞,-1) | B. | (0,1] | C. | (-1,0] | D. | (-1,+∞) |
17.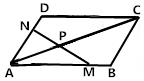 如图,在?ABCD中,M,N分别为AB,AD上的点,且$\overrightarrow{AM}$=$\frac{3}{4}$$\overrightarrow{AB}$,$\overrightarrow{AN}$=$\frac{2}{3}$$\overrightarrow{AD}$,连接AC,MN交于P点,若$\overrightarrow{AP}$=λ$\overrightarrow{AC}$,则λ的值为( )
如图,在?ABCD中,M,N分别为AB,AD上的点,且$\overrightarrow{AM}$=$\frac{3}{4}$$\overrightarrow{AB}$,$\overrightarrow{AN}$=$\frac{2}{3}$$\overrightarrow{AD}$,连接AC,MN交于P点,若$\overrightarrow{AP}$=λ$\overrightarrow{AC}$,则λ的值为( )
 如图,在?ABCD中,M,N分别为AB,AD上的点,且$\overrightarrow{AM}$=$\frac{3}{4}$$\overrightarrow{AB}$,$\overrightarrow{AN}$=$\frac{2}{3}$$\overrightarrow{AD}$,连接AC,MN交于P点,若$\overrightarrow{AP}$=λ$\overrightarrow{AC}$,则λ的值为( )
如图,在?ABCD中,M,N分别为AB,AD上的点,且$\overrightarrow{AM}$=$\frac{3}{4}$$\overrightarrow{AB}$,$\overrightarrow{AN}$=$\frac{2}{3}$$\overrightarrow{AD}$,连接AC,MN交于P点,若$\overrightarrow{AP}$=λ$\overrightarrow{AC}$,则λ的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{7}$ | C. | $\frac{6}{13}$ | D. | $\frac{6}{17}$ |