题目内容
14.已知函数 f(x)=log2(1+x)-log2(1-x).(1)求 f(x)的定义域;
(2)判断 f(x)的奇偶性,并说明理由.
分析 (1)由对数的真数大于0,可得定义域;
(2)函数f(x)是奇函数,计算f(-x)+f(x)是否为0,即可得到结论.
解答 解:(1)由$\left\{\begin{array}{l}{1-x>0}\\{1+x>0}\end{array}\right.$得-1<x<1,
故定义域为(-1,1)…(5分)
(2)函数f(x)是奇函数,证明如下:
∵f(-x)+f(x)=log2(1-x)-log2(x+1)+log2(1+x)-log2(1-x)
=0,
所以,f(x)是奇函数…(12分)
点评 本题考查函数奇偶性的判断,注意运用定义法,考查运算能力,属于基础题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
18.以原点为顶点,x轴为对称轴的抛物线的焦点在直线2x-4y-11=0上,则此抛物线的方程是( )
| A. | y2=11x | B. | y2=-11x | C. | y2=22x | D. | y2=-22x |
5.从[0,2]中任取一个数x,从[0,3]中任取一个数y,则使x2+y2≤4的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{π}{9}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
6.已知三棱锥 S-ABC的所有顶点都在球O的球面上,SA⊥平面ABC,SA=2$\sqrt{3}$,AB=1,AC=2,∠BAC=60°,则球O的体积为( )
| A. | 4π | B. | $\frac{32}{3}π$ | C. | $\frac{16}{3}π$ | D. | 12π |
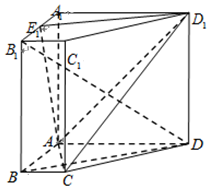 如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,底面ABCD是直角梯形,AD∥BC,∠BAD=90°,AD=AA1=3,BC=1,AB=$\sqrt{3}$,E1为A1B1中点.
如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,底面ABCD是直角梯形,AD∥BC,∠BAD=90°,AD=AA1=3,BC=1,AB=$\sqrt{3}$,E1为A1B1中点. 如图,已知E、F两点分别是正方形ABCD边AD、AB的中点,EF交AC于点M,GC垂直于ABCD所在平面.
如图,已知E、F两点分别是正方形ABCD边AD、AB的中点,EF交AC于点M,GC垂直于ABCD所在平面.