题目内容
10.函数y=ln(ex-x+a)(e为自然对数的底数)的值域是正实数集R+,则实数a的取值范围是( )| A. | (-∞,-1) | B. | (0,1] | C. | (-1,0] | D. | (-1,+∞) |
分析 根据对数的性质,要使值域是正实数集R+,则ex-x+a>1,令g(x)=ex-x+a-1,利用导函数研究其最小值可得结论.
解答 解:函数y=ln(ex-x+a),(ex-x+a>0),
可知,y是增函数,令g(x)=ex-x+a-,值域是正实数集R+,则最小值可以为1,
由g′(x)=ex-1,
当x∈(-∞,0)时,g′(x)<0,则g(x)时单调递减.
当x∈(0,+∞)时,g′(x)>0,则g(x)时单调递增.
故得x=0时,g(x)取得最小值为g(0)=1+a
∴0<1+a≤1,
故得-1<a≤0.
故选C.
点评 本题考查了对数函数的性质及其运用,利用导函数研究函数的最小值问题,属于中档题.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案
相关题目
14.△ABC的顶点A(5,0),B(-5,0),△ABC的周长为22,则顶点C的轨迹方程是( )
| A. | $\frac{x^2}{36}+\frac{y^2}{11}=1$ | B. | $\frac{x^2}{25}+\frac{y^2}{11}=1$ | ||
| C. | $\frac{x^2}{36}+\frac{y^2}{11}=1({y≠0})$ | D. | $\frac{x^2}{9}+\frac{y^2}{16}=1({y≠0})$ |
12.已知x,y满足$\left\{\begin{array}{l}2x-y≥0\\ x+y-1≥0\\ x-2y-1≤0\end{array}\right.$,则$\frac{y-1}{x+1}$的取值范围是( )
| A. | $[-\frac{5}{2},-\frac{1}{4}]$ | B. | $[-\frac{5}{2},2]$ | C. | $[-\frac{1}{2},2)$ | D. | $[-\frac{1}{2},+∞)$ |
5.从[0,2]中任取一个数x,从[0,3]中任取一个数y,则使x2+y2≤4的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{π}{9}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
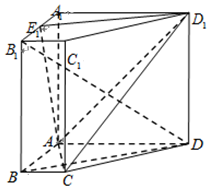 如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,底面ABCD是直角梯形,AD∥BC,∠BAD=90°,AD=AA1=3,BC=1,AB=$\sqrt{3}$,E1为A1B1中点.
如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,底面ABCD是直角梯形,AD∥BC,∠BAD=90°,AD=AA1=3,BC=1,AB=$\sqrt{3}$,E1为A1B1中点.