题目内容
7.甲7:00~8:00到,乙7:20~7:50到,先到者等候另一人10分钟,过时离去.则 求两人会面的概率为$\frac{1}{3}$.分析 由题意知本题是一个几何概型,试验包含的所有事件是Ω={(x,y)|7<x<8,7$\frac{1}{3}$<y<8$\frac{5}{6}$},做出事件对应的集合表示的面积,写出满足条件的事件是A={(x,y)|7<x<8,7$\frac{1}{3}$<y<8$\frac{5}{6}$,|x-y|<$\frac{1}{6}$ },算出事件对应的集合表示的面积,根据几何概型概率公式得到结果
解答 解:设甲到达的时间为x,乙到达的时间为y,则x,y满足Ω={(x,y)|7<x<8,7$\frac{1}{3}$<y<8$\frac{5}{6}$},
所构成的区域为长为1宽为$\frac{5}{6}-\frac{1}{3}=\frac{1}{2}$的矩形,面积为$\frac{1}{2}$;
记“其中一人先到达后最多等候另一人15分钟”为事件A,则A所满足的条件为:A={(x,y)|7<x<8,7$\frac{1}{3}$<y<8$\frac{5}{6}$,|x-y|<$\frac{1}{6}$ },
其面积为$\frac{1}{2}$-$\frac{1}{2}×\frac{1}{2}×\frac{1}{2}$$-\frac{1}{2}×(\frac{1}{6}+\frac{2}{3})×\frac{1}{2}$=$\frac{1}{6}$,
由几何概率的计算公式可得,P(A)=$\frac{\frac{1}{6}}{\frac{1}{2}}=\frac{1}{3}$;
故答案为:$\frac{1}{3}$.
点评 本题主要考查了与面积有关的几何概率的判断及利用几何概率公式求解概率的应用,属于中档试题.

练习册系列答案
相关题目
18.以原点为顶点,x轴为对称轴的抛物线的焦点在直线2x-4y-11=0上,则此抛物线的方程是( )
| A. | y2=11x | B. | y2=-11x | C. | y2=22x | D. | y2=-22x |
2.已知函数f(x)=-x3+ax在区间[-2,1]上是单调增函数,则实数a的最小值是( )
| A. | 12 | B. | 0 | C. | 3 | D. | 1 |
12.已知x,y满足$\left\{\begin{array}{l}2x-y≥0\\ x+y-1≥0\\ x-2y-1≤0\end{array}\right.$,则$\frac{y-1}{x+1}$的取值范围是( )
| A. | $[-\frac{5}{2},-\frac{1}{4}]$ | B. | $[-\frac{5}{2},2]$ | C. | $[-\frac{1}{2},2)$ | D. | $[-\frac{1}{2},+∞)$ |
5.从[0,2]中任取一个数x,从[0,3]中任取一个数y,则使x2+y2≤4的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{π}{9}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
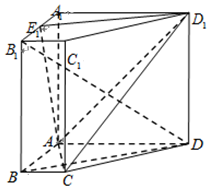 如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,底面ABCD是直角梯形,AD∥BC,∠BAD=90°,AD=AA1=3,BC=1,AB=$\sqrt{3}$,E1为A1B1中点.
如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,底面ABCD是直角梯形,AD∥BC,∠BAD=90°,AD=AA1=3,BC=1,AB=$\sqrt{3}$,E1为A1B1中点.