题目内容
8.一次抛掷两枚骰子,向上点数之和不小于10的概率为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{9}$ | C. | $\frac{2}{9}$ | D. | $\frac{1}{4}$ |
分析 一次投掷两枚骰子,基本事件总数n=6×6=36,利用列举法求出向上点数之和不小于10,包含的基本事件有6个,由此能求出一次抛掷两枚骰子,向上点数之和不小于10的概率.
解答 解:一次投掷两枚骰子,基本事件总数n=6×6=36,
向上点数之和不小于10,包含的基本事件有:
(4,6),(5,5),(5,6),(6,4),(6,5),(6,6),
共有6个,
∴一次抛掷两枚骰子,向上点数之和不小于10的概率为:
p=$\frac{6}{36}$=$\frac{1}{6}$.
故选:A.
点评 本题考查概率的求法,考查古典概型、列举法等基础知识,考查数据处理能力、运算求解能力,考查化归与转化思想、函数与方程思想,是基础题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
18.下列选项叙述错误的是( )
| A. | 命题“若x≠1,则x2-3x+2≠0”的逆否命题是“若x2-3x+2=0,则x=1” | |
| B. | 若命题p:?x∈R,x2+x+1≠0,则?p:?x∈R,x2+x+1=0 | |
| C. | 若p∨q为真命题,则p,q均为真命题 | |
| D. | 若命题q:?x∈R,x2+mx+1>0为真命题,则m的取值范围为-2<m<2 |
19.设a>b,则下列不等式中正确的是( )
| A. | $\frac{1}{a}>\frac{1}{b}$ | B. | a+c>b+c | C. | ac2>bc2 | D. | a2>b2 |
3.已知集合A={1,2,3,4},B={x|x2-3<0},则A∩B=( )
| A. | {1} | B. | {1,2} | C. | {1,2,3} | D. | {1,2,3,4} |
8.等差数列3,1,-1,-3,…,-93的项数为( )
| A. | 52 | B. | 51 | C. | 49 | D. | 50 |
9.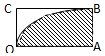 如图,长方形的四个顶点坐标为O(0,0),A(4,0),B(4,2),C(0,2),曲线y=$\sqrt{x}$经过点B,现将质点随机投入长方形OABC中,则质点落在图中阴影部分的概率为( )
如图,长方形的四个顶点坐标为O(0,0),A(4,0),B(4,2),C(0,2),曲线y=$\sqrt{x}$经过点B,现将质点随机投入长方形OABC中,则质点落在图中阴影部分的概率为( )
 如图,长方形的四个顶点坐标为O(0,0),A(4,0),B(4,2),C(0,2),曲线y=$\sqrt{x}$经过点B,现将质点随机投入长方形OABC中,则质点落在图中阴影部分的概率为( )
如图,长方形的四个顶点坐标为O(0,0),A(4,0),B(4,2),C(0,2),曲线y=$\sqrt{x}$经过点B,现将质点随机投入长方形OABC中,则质点落在图中阴影部分的概率为( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{6}$ |
 已知:四棱锥P-ABCD的底面为直角梯形,且AB∥CD,△DAB=90°,DC=2AD=2AB,侧面PAD与底面垂直,PA=PD,点M为侧棱PC上一点D.
已知:四棱锥P-ABCD的底面为直角梯形,且AB∥CD,△DAB=90°,DC=2AD=2AB,侧面PAD与底面垂直,PA=PD,点M为侧棱PC上一点D.