Question

四面体S-ABC中，各个侧面都是边长为a的正三角形，E，F分别是SC和AB的中点，则异面直线EF与SA所成的角等于

 

．

Answer 1

考点：异面直线及其所成的角

专题：空间角

分析：取AC中点O，连结EO，FO，BE，由题意得∠OEF是异面直线EF与SA所成的角（或所成角的补角），由此能求出异面直线EF与SA所成的角．

解答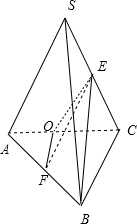： 解：如图，取AC中点O，
连结EO，FO，BE，
则题意知EO∥SA，FO∥BC，
∴∠OEF是异面直线EF与SA所成的角（或所成角的补角），
∵EO=FO=

1

2

a，BE=

a2-( 1 2 a)2

=

3

2

a，
EF=

BE2-BF2

=

3 4 a2- 1 4 a2

=

2

2

a，
∴cos∠OEF=

OE2+EF2-OF2

2OE•EF

=

1 4 a2+ 1 2 a2- 1 4 a2

2• 1 2 a• 2 2 a

=

2

2

，
∴∠OEF=

π

4

．
∴异面直线EF与SA所成的角等于

π

4

．
故答案为：

π

4

．

点评：本题考查异面直线所成角的求法，是基础题，解题时要认真审题，注意空间思维能力的培养．