题目内容
8.已知数列{an},观察程序框图,若k=5,k=10时,分别有S=25,S=100.(1)试求数列{an}的通项;
(2)令${b_n}=n{2^{a_n}}$,求{bn}的前n项和Tn的值.
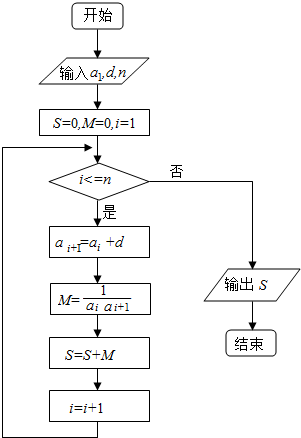
分析 (1)由框图可知{an}为等差数列,设其公差为d,Sn为{an}前n项和,${S_n}=n{a_1}+\frac{n(n-1)d}{2}$,由题意可得$\left\{\begin{array}{l}5{a_1}+10d=25\\ 10{a_1}+45d=100\end{array}\right.$,解得a1,d,即可得通项.
(2)根据(1)的结论,得到${b_n}=n{2^{2n-1}}$,可求等边数列前n项和Tn的值.
解答 解:(1)由框图可知{an}为等差数列,设其公差为d,Sn为{an}前n项和,${S_n}=n{a_1}+\frac{n(n-1)d}{2}$,
由题意得当k=5,k=10时,分别有S=25,S=100,…(3分)
所以$\left\{\begin{array}{l}5{a_1}+10d=25\\ 10{a_1}+45d=100\end{array}\right.$,
解得$\left\{\begin{array}{l}{a_1}=1\\ d=2\end{array}\right.$,
所以an=a1+(n-1)d=2n-1…(6分)
(2)由(1)可得:bn=n22n-1,…(7分),
Tn=1×2+2×23+3×25+…n×22n-1…(1),
4Tn=1×23+2×25+…3×22n-1+n×22n-1…(2)…(8分)
(1)-(2)得:
-3Tn=21+23+25+…+22n-1-n×22n+1
$\begin{array}{l}{\;}=\end{array}\frac{{2(1-{4^n})}}{1-4}-n{2^{2n+1}}$
$\begin{array}{l}{\;}=\end{array}\frac{2}{3}({4^n}-1)-2n{4^n}$.
∴${T_n}=\frac{{2(3n-1){4^n}+2}}{9}$.
点评 本题考查程序框图,数列的概念及简单表示方法,数列的求和,通过对知识的熟练把握,分别进行求值,属于中档题.

 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案| A. | {1,2} | B. | {2,3} | C. | {2,3,4} | D. | {1,2,3,4,6} |
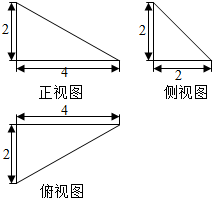
| A. | 4 | B. | 5 | C. | $\frac{9}{2}$ | D. | 6 |