题目内容
14.已知sinx+cosx=$\frac{4\sqrt{2}}{5}$,$\frac{π}{4}$<x<$\frac{π}{2}$,求下列各式的值:(1)sinx•cosx;
(2)cosx-sinx.
分析 根据题意,利用同角三角函数的平方关系式,结合角的取值范围,即可求出结果.
解答 解:∵sinx+cosx=$\frac{4\sqrt{2}}{5}$,$\frac{π}{4}$<x<$\frac{π}{2}$,
∴1>sinx>cosx>0;
(1)∵(sinx+cosx)2=1+2sinxcosx=$\frac{32}{25}$,
∴sinxcosx=$\frac{7}{50}$;
(2)∵cosx-sinx<0,
(cosx-sinx)2=1-2sinxcosx=1-2×$\frac{7}{50}$=$\frac{18}{25}$,
∴cosx-sinx=-$\sqrt{\frac{18}{25}}$=-$\frac{3\sqrt{2}}{5}$.
点评 本题考查了同角三角函数关系的应用问题,解题时应注意角的范围与三角函数值的符号,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.若直线ax+by=1经过圆x2+y2=1内一点,则点(a,b)与此圆的位置关系是( )
| A. | 点在圆上 | B. | 点在圆内 | C. | 点在圆外 | D. | 都有可能 |
9.已知tanα=2,则$\frac{2sinα-cosα}{2sinα+cosα}$=( )
| A. | 1 | B. | $\frac{3}{5}$ | C. | $\frac{1}{3}$ | D. | 0 |
5.椭圆C的中心在原点,焦点在x轴上,离心率等于$\frac{1}{2}$,且它的一个顶点恰好是抛物线x2=8$\sqrt{3}$y的焦点,则椭圆C的标准方程为( )
| A. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1 | B. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1 | C. | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{9}$=1 | D. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1 |
6.椭圆3x2+2y2=6的焦距为( )
| A. | 1 | B. | 2 | C. | $\sqrt{5}$ | D. | $2\sqrt{5}$ |
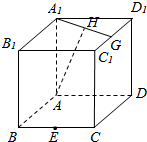 如图,棱长为1的正方体ABCD-A1B1C1D1中,E是BC的中点,F是棱CD上的动点,G为C1D&1的中点,H为A1G的中点.
如图,棱长为1的正方体ABCD-A1B1C1D1中,E是BC的中点,F是棱CD上的动点,G为C1D&1的中点,H为A1G的中点.