题目内容
为了调查某大学学生在周日上网的时间,随机对100名男生和100名女生进行了不记名的问卷调查,
得到了如下的统计结果:
表1:男生上网时间与频数分布表
表2:女生上网时间与频数分布表
(Ⅰ)若该大学共有女生750人,试估计其中上网时间不少于60分钟的人数;
(Ⅱ)完成表3的2×2列联表,并回答能否有90%的把握认为“学生周日上网时间与性别有关”?
(Ⅲ)从表3的男生中“上网时间少于60分钟”和“上网时间不少于60分钟”的人数中用分层抽样的方法抽取一个容量为5的样本,再从中任取两人,求至少有一人上网时间超过60分钟的概率.
表3:
附:k2=
,其中n=a+b+c+d
得到了如下的统计结果:
表1:男生上网时间与频数分布表
| 上网时间(分钟) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80] |
| 人数 | 5 | 25 | 30 | 25 | 15 |
| 上网时间(分钟) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80) |
| 人数 | 10 | 20 | 40 | 20 | 10 |
(Ⅱ)完成表3的2×2列联表,并回答能否有90%的把握认为“学生周日上网时间与性别有关”?
(Ⅲ)从表3的男生中“上网时间少于60分钟”和“上网时间不少于60分钟”的人数中用分层抽样的方法抽取一个容量为5的样本,再从中任取两人,求至少有一人上网时间超过60分钟的概率.
表3:
| 上网时间少于60分钟 | 上网时间不少于60分钟 | 合计 | |
| 男生 | |||
| 女生 | |||
| 合计 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
考点:独立性检验的应用
专题:应用题,概率与统计
分析:(Ⅰ)女生网时间不少于60分钟的人数的比例为
,即可得出结论;
(Ⅱ)根据所给数据完成表3的2×2列联表,利用公式求出k2,与临界值比较,可得结论;
(Ⅲ)容量为5的样本,其中上网时间少于60分钟的有3人,上网时间不少于60分钟有2人,从中任取两人,至少有一人上网时间超过60分钟的概率,利用间接法求解.
| 30 |
| 100 |
(Ⅱ)根据所给数据完成表3的2×2列联表,利用公式求出k2,与临界值比较,可得结论;
(Ⅲ)容量为5的样本,其中上网时间少于60分钟的有3人,上网时间不少于60分钟有2人,从中任取两人,至少有一人上网时间超过60分钟的概率,利用间接法求解.
解答:
解:(Ⅰ)若该大学共有女生750人,估计其中上网时间不少于60分钟的人数750×
=225;
(Ⅱ)完成表3的2×2列联表,
所以k2=
=
=
<2.706,
所以不能有90%的把握认为“学生周日上网时间与性别有关”.
(Ⅲ)从表3的男生中“上网时间少于60分钟”和“上网时间不少于60分钟”的人数中用分层抽样的方法抽取一个容量为5的样本,其中上网时间少于60分钟的有3人,上网时间不少于60分钟有2人.
再从中任取两人,至少有一人上网时间超过60分钟的概率为1-
=
.
| 30 |
| 100 |
(Ⅱ)完成表3的2×2列联表,
| 上网时间少于60分钟 | 上网时间不少于60分钟 | 合计 | |
| 男生 | 60 | 40 | 100 |
| 女生 | 70 | 30 | 100 |
| 合计 | 130 | 70 | 200 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| 200×(60×30-40×70)2 |
| 130×70×100×100 |
| 200 |
| 91 |
所以不能有90%的把握认为“学生周日上网时间与性别有关”.
(Ⅲ)从表3的男生中“上网时间少于60分钟”和“上网时间不少于60分钟”的人数中用分层抽样的方法抽取一个容量为5的样本,其中上网时间少于60分钟的有3人,上网时间不少于60分钟有2人.
再从中任取两人,至少有一人上网时间超过60分钟的概率为1-
| ||
|
| 7 |
| 10 |
点评:本题考查概率知识的运用,考查分层抽样,考查独立性检验知识,考查学生的计算能力,属于中档题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
方程sinx=-cos80°的解集是( )
| A、{X|X=k•180°+10°,k∈z} |
| B、{x|x=k•360°+10°,k∈z} |
| C、{x|x=k•180°±10°,k∈z} |
| D、{x|x=k•180°-(-1)k•10°,k∈z} |
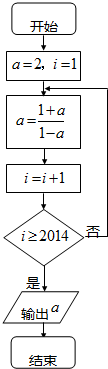
执行如图所示的程序框图,则输出的a的值为( )(注:“a=2”,即为“a←2”或为“a:=2”.)

| A、2 | ||
B、
| ||
C、-
| ||
| D、-3 |