题目内容
11.设平面内有n条直线(n≥3),其中有且仅有两条直线互相平行,任意三条直线不过同一点,若用f(n)表示这n条直线交点的个数,则f(8)的值为( )| A. | 30 | B. | 32 | C. | 27 | D. | 29 |
分析 求出n≥3时f(n)的值,我们要逐一给出f(3),f(4),…,f(n-1),f(n)然后分析项与项之间的关系,然后利用数列求和的办法进行求解,然后求出答案即可.
解答 解:∵f(3)=2,
f(4)=f(3)+3,
f(5)=f(4)+4,
…
f(n-1)=f(n-2)+n-2,
f(n)=f(n-1)+n-1,
累加可得:f(n)=2+3+…+(n-2)+(n-1)=$\frac{1}{2}$(n-2)(n-1+2)=$\frac{1}{2}$(n+1)(n-2),
∴f(8)=$\frac{1}{2}$(8+1)(8-2)=27,
故选:C.
点评 本题考查的知识点是归纳推理与数列求和,根据f(3),f(4),…,f(n-1),f(n)然后分析项与项之间的关系,找出项与项之间的变化趋势是解决问题的关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
19.已知i为虚数单位,复数z=a+bi(a,b∈R)的虚部b记作Im(z),则Im($\frac{-i}{1-i}$)=( )
| A. | -$\frac{1}{2}$ | B. | -1 | C. | $\frac{1}{2}$ | D. | 1 |
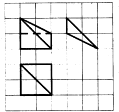 如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体的体积为$\frac{4}{3}$.
如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体的体积为$\frac{4}{3}$. 现给如图所示的4个区域涂色,要求相邻区域不得使用同一颜色,共有3种颜色可供选择,则不同的 涂色方法共有6种.
现给如图所示的4个区域涂色,要求相邻区域不得使用同一颜色,共有3种颜色可供选择,则不同的 涂色方法共有6种.