题目内容
6.计算下列各式的值:(1)8${\;}^{\frac{2}{3}$+(0.01)${\;}^{-\frac{1}{2}}}$+($\frac{1}{27}$)${\;}^{-\frac{1}{3}}$;
(2)21g5+$\frac{2}{3}$lg8+lg5•lg20+(lg2)2.
分析 (1)根据指数幂的运算性质化简即可;
(2)根据对数的运算性质化简即可.
解答 解:(1)8${\;}^{\frac{2}{3}$+(0.01)${\;}^{-\frac{1}{2}}}$+($\frac{1}{27}$)${\;}^{-\frac{1}{3}}$=4+10+3=17
(2)21g5+$\frac{2}{3}$lg8+lg5•lg20+(lg2)2=21g5+2lg2+lg5(1+lg2)+(lg2)2=2+lg5+lg2(lg5+lg2)=2+lg5+lg2=3
点评 本题考查了指数幂和对数的运算性质,属于基础题.

练习册系列答案
相关题目
16.已知全集U=R,A={x|x2-5x+6≥0},则∁UA=( )
| A. | {x|x>2} | B. | {x|x>3或x<2} | C. | {x|2≤x≤3} | D. | {x|2<x<3} |
14.函数f(x)=x2-4x+5在区间[0,m]上的最大值为5,最小值为1,则实数m的取值范围是( )
| A. | [2,+∞) | B. | (2,4] | C. | [0,4] | D. | [2,4] |
18.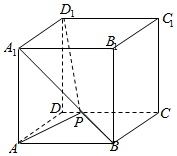 如图棱长为1的正方体ABCD-A1B1C1D1中,P为线段A1B上的动点,则下列结论错误的是( )
如图棱长为1的正方体ABCD-A1B1C1D1中,P为线段A1B上的动点,则下列结论错误的是( )
 如图棱长为1的正方体ABCD-A1B1C1D1中,P为线段A1B上的动点,则下列结论错误的是( )
如图棱长为1的正方体ABCD-A1B1C1D1中,P为线段A1B上的动点,则下列结论错误的是( )| A. | 平面D1A1P⊥平面A1AP | B. | 二面角B-A1D1-A的大小为45° | ||
| C. | 三棱锥B1-D1PC的体积不变 | D. | AP+PD1的最小值为$\sqrt{2+\sqrt{3}}$ |
19.若复数z满足|z|=2,则|1+$\sqrt{3}$i+z|的取值范围是( )
| A. | [1,3] | B. | [1,4] | C. | [0,3] | D. | [0,4] |