题目内容
化简:C
+3C
+5C
+7C
+…+(2n-1)C
= .
1 n |
2 n |
3 n |
4 n |
n n |
考点:二项式定理的应用
专题:计算题,二项式定理
分析:注意观察所求式的结构特点,出现可以应用倒序相加的运算,再等式两边同除以2,得到结论.
解答:
解:设S=C
+3C
+5C
+7C
+…+(2n-1)C
,则
S-1=-1+C
+3C
+5C
+7C
+…+(2n-1)C
,①
则S-1=(2n-1)Cnn+(2n-3)Cnn-1+…+Cn1-1②
①②两式相加,
得2S-2=(2n-2)(Cn0+Cn1+Cn2+…+Cnn)=(2n-2)•2n,
∴Sn=(n-1)•2n+1.
故答案为:(n-1)•2n+1.
1 n |
2 n |
3 n |
4 n |
n n |
S-1=-1+C
1 n |
2 n |
3 n |
4 n |
n n |
则S-1=(2n-1)Cnn+(2n-3)Cnn-1+…+Cn1-1②
①②两式相加,
得2S-2=(2n-2)(Cn0+Cn1+Cn2+…+Cnn)=(2n-2)•2n,
∴Sn=(n-1)•2n+1.
故答案为:(n-1)•2n+1.
点评:本题考查组合与组合数的公式和性质,要用到等差数列求和公式推导的方法,倒序相加,属于中档题.

练习册系列答案
相关题目
按一定规律排列的数列2,5,11,23,47,x,…中的x应为( )
| A、97 | B、95 | C、93 | D、90 |
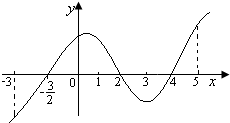 如图是函数y=f(x)的导函数y=f′(x)的图象,对此图象,有如下结论:
如图是函数y=f(x)的导函数y=f′(x)的图象,对此图象,有如下结论: