题目内容
在高台跳水运动中,已知运动员相对于水面的高度h(单位:m)与起跳后的时间t(单位:s)存在函数关系h(t)=-4.9t2+6.5t+10,则运动员在t=1s时的瞬间速度为( )
| A、3.3m/s |
| B、-3.3m/s |
| C、11.6m/s |
| D、-11.6m/s |
考点:变化的快慢与变化率
专题:导数的概念及应用
分析:先求函数h(t)=-4.9t2+6.5t+10的导函数h′(t),由导数的物理意义,函数h′(t)即为t时刻运动员的瞬时速度,故将t=1代入计算即可
解答:
解:∵h(t)=-4.9t2+6.5t+10,
∴h′(t)=-9.8t+6.5
∴h′(1)=-9.8+6.5=-3.3
∴起跳后1s的瞬时速度是-3.3m/s
故选:B.
∴h′(t)=-9.8t+6.5
∴h′(1)=-9.8+6.5=-3.3
∴起跳后1s的瞬时速度是-3.3m/s
故选:B.
点评:本题考察了导数的物理意义,导数的基本运算,辨清位移函数与瞬时速度的关系是解决本题的关键

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
已知a<b<0,则下列不等式一定成立的是( )
A、
| ||||
| B、|a|>-b | ||||
C、
| ||||
D、
|
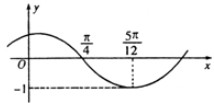 f(x)=Asin(ωx+φ),(A>0,ω>0,|φ|<
f(x)=Asin(ωx+φ),(A>0,ω>0,|φ|<| π |
| 2 |
A、向右平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向左平移
|
若直线l1:y=kx+1与l2:x-y-1=0的交点在第一象限内,则k的取值范围是( )
| A、k>1 |
| B、-1<k<1 |
| C、k<-1或k>1 |
| D、k<-1 |
如图,D是直角△ABC斜边BC上一点,若AB=AD,AC=
DC,则sin∠ABD=( )
| 3 |

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
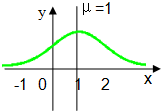 在对我市高中学生某项身体素质的测试中,测试结果ξ服从正态分布N(1,σ2)(σ>0)(如图),若ξ在(0,2)内取值的概率为0.8,则ξ在(0,1)内取值的概率为
在对我市高中学生某项身体素质的测试中,测试结果ξ服从正态分布N(1,σ2)(σ>0)(如图),若ξ在(0,2)内取值的概率为0.8,则ξ在(0,1)内取值的概率为