题目内容
若圆B:x2+y2+b=0与圆C:x2+y2-6x+8y+16=0没有公共点,则b的取值范围是 .
考点:圆与圆的位置关系及其判定
专题:直线与圆
分析:由题意可得,两个圆相离或相内含,若两个圆相离,则由两个圆的圆心距d大于两个圆的半径之和,求得b的范围.若两个圆相内含,则由两个圆的圆心距d小于两个圆的半径之差,求得b的范围,再把这2个b的范围取并集,即得所求.
解答:
解:圆B:x2+y2+b=0表示圆心为O(0,0)、半径等于
的圆,(b<0);
圆C:x2+y2-6x+8y+16=0即 (x-3)2+(y+4)2=9 表示圆心为(3,-4)、半径等于3的圆.
由题意可得,两个圆相离或相内含.
若两个圆相离,则由两个圆的圆心距d大于两个圆的半径之和,即
>3+
,
求得-4<b<0.
若两个圆相内含,则由两个圆的圆心距d小于两个圆的半径之差,即
<|3-
|,
求得b<-64,
故答案为:{b|-4<b<0,或b<-64}.
| -b |
圆C:x2+y2-6x+8y+16=0即 (x-3)2+(y+4)2=9 表示圆心为(3,-4)、半径等于3的圆.
由题意可得,两个圆相离或相内含.
若两个圆相离,则由两个圆的圆心距d大于两个圆的半径之和,即
| 9+16 |
| -b |
求得-4<b<0.
若两个圆相内含,则由两个圆的圆心距d小于两个圆的半径之差,即
| 9+16 |
| -b |
求得b<-64,
故答案为:{b|-4<b<0,或b<-64}.
点评:本题主要考查圆的标准方程,两个圆的位置关系的判定方法,体现了分类讨论的数学思想,属于基础题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
已知a<b<0,则下列不等式一定成立的是( )
A、
| ||||
| B、|a|>-b | ||||
C、
| ||||
D、
|
对于函数y=sin(2x),下面说法中正确的是( )
| A、函数是周期为π的奇函数 |
| B、函数是周期为π的偶函数 |
| C、函数是周期为2π的奇函数 |
| D、函数是周期为2π的偶函数 |
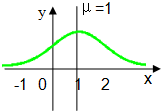 在对我市高中学生某项身体素质的测试中,测试结果ξ服从正态分布N(1,σ2)(σ>0)(如图),若ξ在(0,2)内取值的概率为0.8,则ξ在(0,1)内取值的概率为
在对我市高中学生某项身体素质的测试中,测试结果ξ服从正态分布N(1,σ2)(σ>0)(如图),若ξ在(0,2)内取值的概率为0.8,则ξ在(0,1)内取值的概率为