题目内容
已知β∈(0,π),cosβ=-
,则
= .
| 24 |
| 25 |
| 1 |
| tanβ |
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:由cosβ的值以及β的范围,利用同角三角函数间的基本关系求出sinβ的值,即可确定出tanβ的值.
解答:
解:∵β∈(0,π),cosβ=-
,
∴sinβ=
=
,
∴tanβ=
=-
,
则
=-
.
故答案为:-
.
| 24 |
| 25 |
∴sinβ=
| 1-cos2β |
| 7 |
| 25 |
∴tanβ=
| sinβ |
| cosβ |
| 7 |
| 24 |
则
| 1 |
| tanβ |
| 24 |
| 7 |
故答案为:-
| 24 |
| 7 |
点评:此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
相关题目
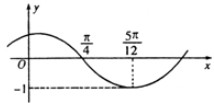 f(x)=Asin(ωx+φ),(A>0,ω>0,|φ|<
f(x)=Asin(ωx+φ),(A>0,ω>0,|φ|<| π |
| 2 |
A、向右平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向左平移
|
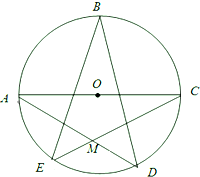 如图,已知A,B,C,D,E均在⊙O上,且AC为⊙O的直径.
如图,已知A,B,C,D,E均在⊙O上,且AC为⊙O的直径.