题目内容
1.甲、乙二人进行乒乓球比赛,先胜4局者为胜,甲每局中获胜的概率为$\frac{3}{5}$.(1)求甲以4:1获胜的概率;
(2)求比赛局数不多于5局的概率.
分析 (1)甲以4:1获胜是指甲前4局比赛中3胜1负,第5局比赛甲胜,由此能求出甲以4:1获胜的概率.
(2)比赛局数不多于5局包含四种情况:①甲以4:0获胜;②甲以4:1获胜;③乙以4:0获胜;④乙以4:1获胜.由此能求出比赛局数不多于5局的概率.
解答 解:(1)∵甲、乙二人进行乒乓球比赛,先胜4局者为胜,甲每局中获胜的概率为$\frac{3}{5}$,
∴甲以4:1获胜是指甲前4局比赛中3胜1负,第5局比赛甲胜,
∴甲以4:1获胜的概率:p=${C}_{4}^{1}(\frac{3}{5})^{3}(\frac{2}{5})$•($\frac{3}{5}$)=$\frac{648}{3125}$.
(2)比赛局数不多于5局包含四种情况:
①甲以4:0获胜;②甲以4:1获胜;③乙以4:0获胜;④乙以4:1获胜.
∴比赛局数不多于5局的概率:
p=($\frac{3}{5}$)4+${C}_{4}^{1}(\frac{3}{5})^{3}(\frac{2}{5})$•($\frac{3}{5}$)+($\frac{2}{5}$)4+${C}_{4}^{1}(\frac{2}{5})^{3}(\frac{3}{5})•(\frac{2}{5})$=$\frac{53}{125}$.
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意n次独立重复试验中事件A恰好发生k次的概率计算公式的合理运用.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
11.设集合A=$\left\{{\left.x\right|\frac{1}{2}<x<3}\right\}$,B={x|(x+1)(x-2)<0},则A∪B=( )
| A. | $\left\{{\left.x\right|\frac{1}{2}<x<2}\right\}$ | B. | {x|-1<x<3} | C. | $\left\{{\left.x\right|\frac{1}{2}<x<1}\right\}$ | D. | {x|1<x<2} |
9.已知数列{an}的首项a1=a,其前n项和为Sn,且满足Sn+Sn-1=4n2(n≥2,n∈N+),若对任意n∈N+,an<an+1恒成立,则a的取值范围是( )
| A. | (3,5) | B. | (4,6) | C. | [3,5) | D. | [4,6) |
10.已知离散型随机变量ξ的概率分布为
则P(ξ=2)=0.52.
| ξ | 0 | 1 | 2 | 3 |
| P | 0.12 | 0.24 | 0.12 |
11.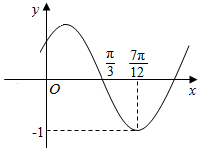 函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,将函数f(x)的图象向右平移$\frac{π}{6}$个单位后得到的函数图象的解析式为( )
函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,将函数f(x)的图象向右平移$\frac{π}{6}$个单位后得到的函数图象的解析式为( )
 函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,将函数f(x)的图象向右平移$\frac{π}{6}$个单位后得到的函数图象的解析式为( )
函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,将函数f(x)的图象向右平移$\frac{π}{6}$个单位后得到的函数图象的解析式为( )| A. | y=sin2x | B. | y=sin(2x+$\frac{π}{3}$) | C. | y=sin(2x+$\frac{π}{6}$) | D. | y=sin(2x-$\frac{π}{3}$) |