题目内容
16．已知数列{an}，a1=20，an=an+1+2，求：（1）a5的值；
（2）数列{an}的前n项和Sn．
分析 （1）易得数列为等差数列，由首项和公差可得通项公式，当n=5时，求得a5=12；
（2）根据等差数列的首项和公差即可写出数列的前n项和．
解答 解：（1）数列{an}，a1=20，an=an+1+2，an+1-an=-2，
数列{an}是以20为首项，以-2为公差的等差数列，
an=20-2（n-1）=-2n+22，
∴an=-2n+22，
当n=5时，a5=12；
（2）数列{an}的前n项和Sn，Sn=$\frac{n（20-2n+22）}{2}$=（21-n）n，
∴Sn=（21-n）n．
点评 本题考查等差数列的通项公式和前n项和公式，属基础题．
练习册系列答案
53随堂测系列答案
相关题目
6．已知为虚数单位，复数z满足z=$\frac{1+i}{1-i}$，则z2=（ ）
| A． | 1 | B． | -1 | C． | 2i | D． | -2i |
4．设等比数列{an}的通项为an=$\frac{1}{n（n+1）}$，则其前10项的和S10等于（ ）
| A． | $\frac{9}{10}$ | B． | $\frac{11}{10}$ | C． | $\frac{10}{9}$ | D． | $\frac{10}{11}$ |
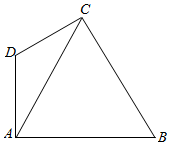滨湖区拟建一主题游戏园，该游戏园为四边形区域ABCD，其中三角形区城ABC为主题活动区，其中∠ACB=60°，∠ABC=45°，AB=12$\sqrt{6}$m；AD、CD为游客通道（不考虑宽度），且∠ADC=120°，通道AD、CD围成三角形区域ADC为游客休闲中心，供游客休憩．