题目内容
如图正方体ABCD-A1B1C1D1中,试用三种方法求A1C与BC1所成角的余弦值.
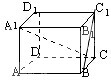

考点:异面直线及其所成的角
专题:空间角
分析:解法一:线面垂直方法;
解法二:建立空间直角坐标系,向量法;
解法三:补形法(平移法).
解法二:建立空间直角坐标系,向量法;
解法三:补形法(平移法).
解答:
解法一:如图所示, 连接B1C,A1E.
连接B1C,A1E.
则A1B1⊥BC1,BC1⊥B1C,
∵A1B1∩B1C=B1,
∴BC1⊥平面A1B1CD,
∴BC1⊥A1C,
∴A1C与BC1所成角的余弦值=0.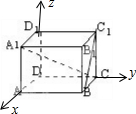
解法二:如图所示,建立空间直角坐标系.
不妨设AB=1.则A1(1,0,1),B(1,1,0),C(0,1,0),C1(0,1,1).
∴
=(-1,1,-1),
=(-1,0,1).
∴
•
=1+0-1=0,
∴A1C与BC1所成角的余弦值为0.
解法三:如图所示, 在正方体ABCD-A1B1C1D1后面再补一个与之全等的正方体.
在正方体ABCD-A1B1C1D1后面再补一个与之全等的正方体.
连接CF,A1F.
不妨设AB=1,则A1C=
,CF=
,
A1F=
.
∴A1C2+CF2=A1F2.
∴A1C⊥CF.
∴A1C⊥BC1.
∴A1C与BC1所成角的余弦值为0.
 连接B1C,A1E.
连接B1C,A1E.则A1B1⊥BC1,BC1⊥B1C,
∵A1B1∩B1C=B1,
∴BC1⊥平面A1B1CD,
∴BC1⊥A1C,
∴A1C与BC1所成角的余弦值=0.

解法二:如图所示,建立空间直角坐标系.
不妨设AB=1.则A1(1,0,1),B(1,1,0),C(0,1,0),C1(0,1,1).
∴
| A1C |
| BC1 |
∴
| A1C |
| BC1 |
∴A1C与BC1所成角的余弦值为0.
解法三:如图所示,
 在正方体ABCD-A1B1C1D1后面再补一个与之全等的正方体.
在正方体ABCD-A1B1C1D1后面再补一个与之全等的正方体.连接CF,A1F.
不妨设AB=1,则A1C=
| 3 |
| 2 |
A1F=
| 5 |
∴A1C2+CF2=A1F2.
∴A1C⊥CF.
∴A1C⊥BC1.
∴A1C与BC1所成角的余弦值为0.
点评:本题考查了利用多种方法求异面直线所成的角、正方体的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目