题目内容
已知角α的终边经过点P0（-3，-4），则cosα的值为（ ）
A、-
| ||
B、
| ||
C、
| ||
D、-
|
考点：任意角的三角函数的定义
专题：三角函数的求值
分析：根据角α的终边经过点P0（-3，-4），利用任意角的三角函数定义求出cosα的值．
解答：
解：∵角α的终边经过点P0（-3，-4），
∴cosα=
=-
，
故选：D．
∴cosα=
| -3 | ||
|
| 3 |
| 5 |
故选：D．
点评：此题考查了运用诱导公式化简求值，以及任意角的三角函数定义，熟练掌握诱导公式是解本题的关键．
练习册系列答案
相关题目
下列推理正确的是（ ）
| A、如果不买彩票，那么就不能中奖．因为你买了彩票，所以你一定中奖 | ||||||||||||||
| B、因为a＞b，a＞c，所以a-b＞a-c | ||||||||||||||
C、若a＞0，b＞0，则lga+lgb≥2
| ||||||||||||||
D、若a＞0，b＜0，则
|
已知f（x）=log
（x2-2x）的单调递增区间是（ ）
| 1 |
| 2 |
| A、（1，+∞） |
| B、（2，+∞） |
| C、（-∞，0） |
| D、（-∞，1） |
抛掷两颗骰子，第一颗骰子向上的点数为x，第二颗骰子向上的点数为y，则“|x-y|＞1”的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
定义在R上的函数f（x）对于定义域内任意x1，x2（x1≠x2）都有（x1-x2）[f（x1）-f（x2）]＞0成立，且函数f（x）对于任意的x都有f（x）=-f（2-x）恒成立，如果实数m，n满足条件f（m2-6m+23）+f（n2-8n）＜0且m＞3，那么m2+n2的取值范围是（ ）
| A、（13，49） |
| B、（13，45） |
| C、（9，25） |
| D、（9，49） |
在数学归纳法的递推性证明中由假设n=k时成立推导n=k+1时成立时f（n）=1+
+
+…+
增加的项数是（ ）
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2n-1 |
| A、1 |
| B、2k+1 |
| C、2k-1 |
| D、2k |
已知函数y=xlnx，则这个函数在点（1，0）处的切线方程是（ ）
| A、y=2x-2 |
| B、y=2x+2 |
| C、y=x-1 |
| D、y=x+1 |
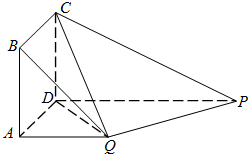在如图所示的多面体中，四边形ABCD为正方形，四边形ADPQ是直角梯形，AD⊥DP，CD⊥平面PDAQ，AB=AQ=