题目内容
如图,四棱锥P-ABCD中,PA⊥平面ABCD,E为BD的中点,G为PD的中点,△DAB ≌△DCB,EA=EB=AB=1,PA= ,连接CE并延长交AD于F.
,连接CE并延长交AD于F.
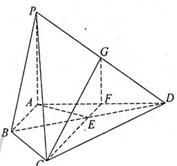
(1)求证:AD⊥平面CFG;
(2)求平面BCP与平面DCP的夹角的余弦值.
 ,连接CE并延长交AD于F.
,连接CE并延长交AD于F.
(1)求证:AD⊥平面CFG;
(2)求平面BCP与平面DCP的夹角的余弦值.
(1)见解析 (2)

(1)因为△DAB ≌△DCB,EA=EB=AB=1,所以△ECB是等边, ,
,

(2)建立空间坐标系如图,

取向观点的坐标为 , 向量
, 向量
 设平面PBC的法向量
设平面PBC的法向量 平面PDC的法向量
平面PDC的法向量 则
则

 ,
,
(2)建立空间坐标系如图,

取向观点的坐标为
 , 向量
, 向量 设平面PBC的法向量
设平面PBC的法向量 平面PDC的法向量
平面PDC的法向量 则
则

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的边长为2,
的边长为2, ,
, 分别为
分别为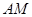 ,
,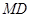 的中点,在五棱锥
的中点,在五棱锥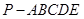 中,
中,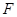 为棱
为棱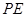 的中点,平面
的中点,平面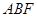 与棱
与棱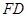 ,
,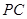 分别交于
分别交于 ,
,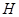 .
.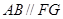 ;
;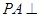 底面
底面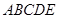 ,且
,且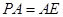 ,求直线
,求直线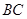 与平面
与平面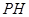 的长.
的长.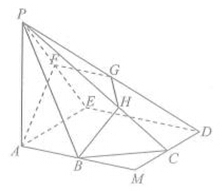
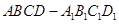 底面
底面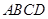 直角梯形,
直角梯形,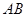 ∥
∥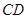 ,
,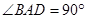 ,
,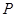 是棱
是棱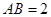 ,
,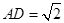 ,
,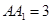 ,
,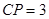 ,
,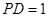 .
.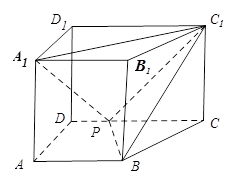
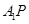 与
与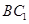 所成的角;
所成的角;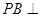 平面
平面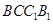 .
.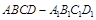 中,底面
中,底面 是矩形,
是矩形,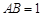 ,
,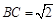 ,
,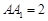 ,
,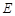 是侧棱
是侧棱 的中点.
的中点.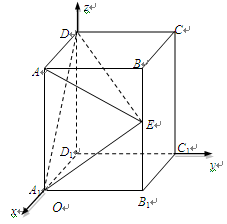
 平面
平面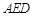 ;
;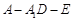 的大小.
的大小.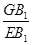 中,已知
中,已知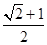 ,
,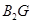 ,
,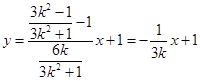 .
.
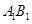 与
与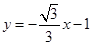 夹角的余弦值;
夹角的余弦值;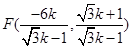 平面角的余弦值.
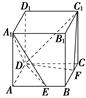
平面角的余弦值. 中,侧面
中,侧面
 底面
底面 ,
, ,底面
,底面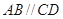 ,
,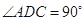 ,
,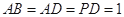 ,
,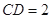 .
.
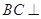 平面
平面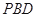 ;
;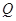 为侧棱
为侧棱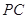 上一点,
上一点,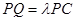 ,试确定
,试确定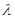 的值,使得二面角
的值,使得二面角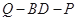 为
为 .
.

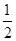
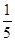

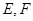 分别是
分别是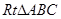 的斜边
的斜边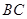 上的两个三等分点,已知
上的两个三等分点,已知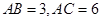 ,则
,则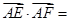 .
.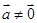 ,
,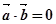 ,则
,则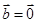 ; ②若
; ②若 ,则
,则 ;
;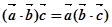 ; ④
; ④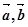 为非零不共线,若
为非零不共线,若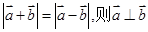 ;
;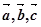 非零不共线,则
非零不共线,则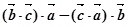 与
与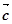 垂直
垂直