题目内容
已知函数f(x)是定义域为R的单调减函数,且是奇函数,当x>0时,f(x)=
-2x
(1)求f(x)的解析式;
(2)解关于t的不等式f[lg(t+1)]+f[1-lgt]<0.
| x |
| 3 |
(1)求f(x)的解析式;
(2)解关于t的不等式f[lg(t+1)]+f[1-lgt]<0.
考点:函数单调性的性质,函数解析式的求解及常用方法
专题:计算题,函数的性质及应用
分析:(1)由奇函数的性质求出f(x)的解析式;(2)由函数的单调性解不等式.
解答:
解:(1)∵f(x)是定义域为R的奇函数,
∴f(0)=0;
当x<0时,-x>0,则
f(x)=-f(-x)=-(-
-2-x)
=
+2-x
∴f(x)=
,
(2)∵f[lg(t+1)]+f[1-lgt]<0,
∴f[lg(t+1)]<f[lgt-1],
∵f(x)是定义域为R的单调减函数,
∴lg(t+1)>lgt-1,
∴
>0,t+1>0,且t+1>
;
解得,t>-1.
∴不等式的解集是(-1,+∞).
∴f(0)=0;
当x<0时,-x>0,则
f(x)=-f(-x)=-(-
| x |
| 3 |
=
| x |
| 3 |
∴f(x)=
|
(2)∵f[lg(t+1)]+f[1-lgt]<0,
∴f[lg(t+1)]<f[lgt-1],
∵f(x)是定义域为R的单调减函数,
∴lg(t+1)>lgt-1,
∴
| t |
| 10 |
| t |
| 10 |
解得,t>-1.
∴不等式的解集是(-1,+∞).
点评:本题考查了奇偶性与单调性的综合应用,属于中档题.

练习册系列答案
相关题目
 莆田往福州的某次动车途中经停福清站,为了方便莆田市VIP客户搭乘,车站信息管理员对该次动车VIP车厢(共4个座位)莆田至福州的全程空座位数n进行统计,得到10个车次样本数据的茎叶图,如图所示.(全程空座位数即莆田至福清、福清至福州两个站段的空座位数之和)
莆田往福州的某次动车途中经停福清站,为了方便莆田市VIP客户搭乘,车站信息管理员对该次动车VIP车厢(共4个座位)莆田至福州的全程空座位数n进行统计,得到10个车次样本数据的茎叶图,如图所示.(全程空座位数即莆田至福清、福清至福州两个站段的空座位数之和)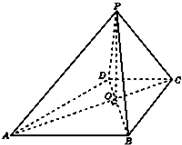 如图,已知四棱锥P-ABCD的底面ABCD为等腰梯形,AB∥DC,AC⊥BD,AC与BD相交于点O,且顶点P在底面上的射影恰为O点,又BO=2,PO=
如图,已知四棱锥P-ABCD的底面ABCD为等腰梯形,AB∥DC,AC⊥BD,AC与BD相交于点O,且顶点P在底面上的射影恰为O点,又BO=2,PO=