题目内容
9.(1)求曲线y=x3-x在点A(1,0)处的切线方程;(2)求经过点B($\frac{π}{3}$,$\frac{1}{2}$)且与曲线y=cosx相切的直线方程.
分析 (1)求出导数,求得切线的斜率,运用点斜式方程即可得到所求切线的方程;
(2)判断点B在曲线y=cosx上,且为切点,求得切线的斜率,运用点斜式方程即可得到所求切线方程.
解答 解:(1)∵f(1)=13-1=0,
∴点A(1,0)在y=x3-x上.
又∵y′=3x2-1,∴k=f′(1)=3-1=2,
∴切线方程为:y-0=2(x-1),即2x-y-2=0.
(2)∵cos $\frac{π}{3}$=$\frac{1}{2}$,∴点B($\frac{π}{3}$,$\frac{1}{2}$)在y=cosx上,且为切点.
又∵f′(x)=(cosx)′=-sinx,
∴f′($\frac{π}{3}$)=-sin$\frac{π}{3}$=-$\frac{\sqrt{3}}{2}$,
∴切线方程为:
y-$\frac{1}{2}$=-$\frac{\sqrt{3}}{2}$ (x-$\frac{π}{3}$),
即$\frac{\sqrt{3}}{2}$x+y-$\frac{1}{2}$-$\frac{\sqrt{3}}{6}π$=0.
点评 本题考查导数的运用:求切线方程,正确求导和运用点斜式方程是解题的关键,属于基础题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
20.集合A={y|y=x-2},B={y|y=$\sqrt{x}$},则x∈A是x∈B的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 不充分不必要条件 |
14.函数y=log(x-2)(5-x)的定义域是( )
| A. | (3,4) | B. | (2,5) | C. | (2,3)∪(3,5) | D. | (-∞,2)∪(5,+∞) |
1.已知α,β为锐角△ABC的两个内角,x∈R,f(x)=($\frac{cosα}{sinβ}$)|x-2|+($\frac{cosβ}{sinα}$)|x-2|,则关于x的不等式f(2x-1)-f(x+1)>0的解集为( )
| A. | (-∞,$\frac{4}{3}$)∪(2,+∞) | B. | ($\frac{4}{3}$,2) | C. | (-∞,-$\frac{4}{3}$)∪(2,+∞) | D. | (-$\frac{4}{3}$,2) |
 已知奇函数$f(x)=\left\{{\begin{array}{l}{-{x^2}+2x}\\ 0\\{{x^2}+2x}\end{array}\begin{array}{l}{({x>0})}\\{({x=0})}\\{({x<0})}\end{array}}\right.$
已知奇函数$f(x)=\left\{{\begin{array}{l}{-{x^2}+2x}\\ 0\\{{x^2}+2x}\end{array}\begin{array}{l}{({x>0})}\\{({x=0})}\\{({x<0})}\end{array}}\right.$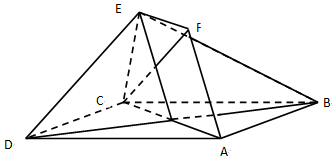 (文)如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,EF=CE,AB=$\sqrt{2}$EF.
(文)如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,EF=CE,AB=$\sqrt{2}$EF.