题目内容
函数f(x)=[x]的函数值表示不超过x的最大整数,例如,[-3.5]=-4,[2.1]=2,当x∈(-2.5,3]时.
①写出函数f(x)的解析式;②作出函数f(x)的图象;
③若直线y=mx与函数f(x)=[x],x∈(-2.5,3]的图象有且仅有2个公共点,求m的取值范围.
①写出函数f(x)的解析式;②作出函数f(x)的图象;
③若直线y=mx与函数f(x)=[x],x∈(-2.5,3]的图象有且仅有2个公共点,求m的取值范围.
考点:函数的图象,根的存在性及根的个数判断
专题:函数的性质及应用
分析:①根据f(x)=[x]的定义,利用分段函数求出函数的解析式,
②作出对应的图象即可.
③根据图象,求出直线y=mx过特殊点的斜率,继而求出m的范围
②作出对应的图象即可.
③根据图象,求出直线y=mx过特殊点的斜率,继而求出m的范围
解答:
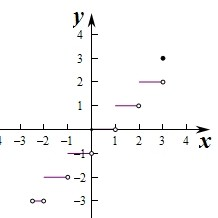 解:①根据函数f(x)=[x]的定义可知:
解:①根据函数f(x)=[x]的定义可知:
当-2.5<x<-2时,f(x)=-3,
当-2≤x<-1时,f(x)=-2,
当-1≤x<0时,f(x)=-1,
当0≤x<1时,f(x)=0,
当1≤x<2时,f(x)=1,
当2≤x<3时,f(x)=2,
当x=3时,f(x)=3,
即
f(x)=
,
②对应的图象如右图所示:
③直线y=mx是过原点的一条直线,如图所示
当直线过点A时,m=
,此时一个交点,
当直线过点B时,m=
,此时一个交点,
由图可以看出当
<m<
时,有两个交点,
当直线过点D时,m=2,此时两个交点,
由图可以看出当m>2时,有两个交点,
综上所述:m的取值范围为(
,
)∪[2,+∞)
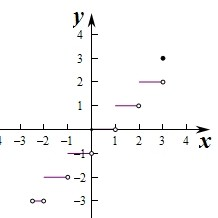 解:①根据函数f(x)=[x]的定义可知:
解:①根据函数f(x)=[x]的定义可知:当-2.5<x<-2时,f(x)=-3,
当-2≤x<-1时,f(x)=-2,
当-1≤x<0时,f(x)=-1,
当0≤x<1时,f(x)=0,
当1≤x<2时,f(x)=1,
当2≤x<3时,f(x)=2,
当x=3时,f(x)=3,
即
f(x)=
|
②对应的图象如右图所示:

③直线y=mx是过原点的一条直线,如图所示
当直线过点A时,m=
| 1 |
| 2 |
当直线过点B时,m=
| 2 |
| 3 |
由图可以看出当
| 1 |
| 2 |
| 2 |
| 3 |
当直线过点D时,m=2,此时两个交点,
由图可以看出当m>2时,有两个交点,
综上所述:m的取值范围为(
| 1 |
| 2 |
| 2 |
| 3 |
点评:本题主要考查函数解析式的求法,利用函数的定义建立函数关系是解决本题的关键,以及分段函数的画法与交点的个数问题,属于中档题

练习册系列答案
相关题目
如图是某样本数据的茎叶图,则该样本数据的众数为( )
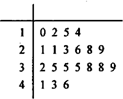

| A、10 | B、21 | C、35 | D、46 |
已知集合M={x||x-1|<1},集合N={x|x2-2x<3},则M∩∁RN=( )
| A、{x|0<x<2} |
| B、{x|-1<x<2} |
| C、{x|-1<x≤0或2≤x<3} |
| D、∅ |