题目内容
14.以$F(0,\frac{p}{2})(p>0)$为焦点的抛物线C的准线与双曲线x2-y2=2相交于M,N两点,若△MNF为正三角形,则抛物线C的方程为( )| A. | ${y^2}=2\sqrt{6}x$ | B. | ${y^2}=4\sqrt{6}x$ | C. | ${x^2}=2\sqrt{6}y$ | D. | ${x^2}=4\sqrt{6}y$ |
分析 由题意,y=$\frac{p}{2}$代入双曲线x2-y2=2,可得x=±$\sqrt{2+\frac{{p}^{2}}{4}}$,利用△MNF为正三角形,求出p,即可求出抛物线的方程.
解答 解:由题意,y=$\frac{p}{2}$代入双曲线x2-y2=2,可得x=±$\sqrt{2+\frac{{p}^{2}}{4}}$,
∵△MNF为正三角形,
∴p=$\frac{\sqrt{3}}{2}$×2$\sqrt{2+\frac{{p}^{2}}{4}}$,
∵p>0,∴p=2$\sqrt{6}$,
∴抛物线C的方程为x2=4$\sqrt{6}$y,
故选:D.
点评 本题考查抛物线的简单性质,双曲线方程的应用,考查分析问题解决问题的能力以及计算能力.

练习册系列答案
相关题目
4.设Sn为等比数列{an}的前n项和,若S1,S3,S2成等差数列,则等比数列{an}的公比q=( )
| A. | -2 | B. | -1 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
2.已知函数$f(x)=asinxcosx-{sin^2}x+\frac{1}{2}$的一条对称轴方程为$x=\frac{π}{6}$,则函数f(x)的单调递增区间为( )
| A. | $[{kπ-\frac{π}{3},kπ+\frac{π}{6}}]$,(k∈Z) | B. | $[{kπ-\frac{π}{12},kπ+\frac{5π}{12}}]$,(k∈Z) | ||
| C. | $[{kπ-\frac{7π}{12},kπ-\frac{π}{12}}]$,(k∈Z) | D. | $[{kπ+\frac{π}{6},kπ+\frac{2π}{3}}]$,(k∈Z) |
19.已知变量x,y满足$\left\{\begin{array}{l}x-y≥-2\\ x+y≥-2\\ x≤0\end{array}\right.$则$\frac{y+2}{x+3}$的最大值为( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | 1 |
6.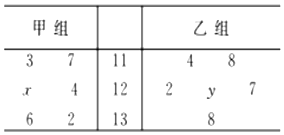 如图茎叶图记录了甲、乙两组各6名学生在一次数学测试中的成绩(单位:分),已知甲组数据的众数为124,乙组数据的平均数为甲组数据的中位数,则x,y的值分别为( )
如图茎叶图记录了甲、乙两组各6名学生在一次数学测试中的成绩(单位:分),已知甲组数据的众数为124,乙组数据的平均数为甲组数据的中位数,则x,y的值分别为( )
 如图茎叶图记录了甲、乙两组各6名学生在一次数学测试中的成绩(单位:分),已知甲组数据的众数为124,乙组数据的平均数为甲组数据的中位数,则x,y的值分别为( )
如图茎叶图记录了甲、乙两组各6名学生在一次数学测试中的成绩(单位:分),已知甲组数据的众数为124,乙组数据的平均数为甲组数据的中位数,则x,y的值分别为( )| A. | 4,4 | B. | 5,4 | C. | 4,5 | D. | 5,5 |
4.已知复数z满足z(2+i)=3+2i,则|z|=( )
| A. | $\sqrt{3}$ | B. | $\sqrt{13}$ | C. | $\frac{\sqrt{65}}{5}$ | D. | $\sqrt{15}$ |