题目内容
4.设Sn为等比数列{an}的前n项和,若S1,S3,S2成等差数列,则等比数列{an}的公比q=( )| A. | -2 | B. | -1 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
分析 依题意有a1+(a1+a1q)=2(a1+a1q+a1q2),从而2q2+q=0,由此能求出{an}的公比q.
解答 解:∵等比数列{an}的前n项和为Sn,S1,S3,S2成等差数列,
即为2S3=S1+S2,
依题意有a1+(a1+a1q)=2(a1+a1q+a1q2),
由于a1≠0,故2q2+q=0,
又q≠0,解得q=-$\frac{1}{2}$.
故选:C.
点评 本题考查等比数列的公比的求法,是基础题,解题时要注意等差数列和等比数列的性质的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.已知集合M={1,2},N={2,3,4},若P=M∪N,则P的子集个数为( )
| A. | 14 | B. | 15 | C. | 16 | D. | 32 |
9.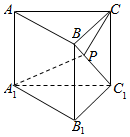 如图,在三棱柱ABC-A1B1C1中,CC1⊥底面A1B1C1,且A1C1⊥B1C1,A1C1=3$\sqrt{2}$,B1C1=CC1=2,P是BC1上一动点,则CP+PA1的最小值为( )
如图,在三棱柱ABC-A1B1C1中,CC1⊥底面A1B1C1,且A1C1⊥B1C1,A1C1=3$\sqrt{2}$,B1C1=CC1=2,P是BC1上一动点,则CP+PA1的最小值为( )
 如图,在三棱柱ABC-A1B1C1中,CC1⊥底面A1B1C1,且A1C1⊥B1C1,A1C1=3$\sqrt{2}$,B1C1=CC1=2,P是BC1上一动点,则CP+PA1的最小值为( )
如图,在三棱柱ABC-A1B1C1中,CC1⊥底面A1B1C1,且A1C1⊥B1C1,A1C1=3$\sqrt{2}$,B1C1=CC1=2,P是BC1上一动点,则CP+PA1的最小值为( )| A. | 5$\sqrt{2}$ | B. | 5 | C. | $\sqrt{10}$ | D. | $\sqrt{34}$ |
13.已知α,β均为锐角,且cos(α+β)=ncos(α-β),则tanαtanβ=( )
| A. | $\frac{1-n}{1+n}$ | B. | $\frac{1+n}{1-n}$ | C. | $\frac{n-1}{1+n}$ | D. | $\frac{1+n}{n-1}$ |
14.以$F(0,\frac{p}{2})(p>0)$为焦点的抛物线C的准线与双曲线x2-y2=2相交于M,N两点,若△MNF为正三角形,则抛物线C的方程为( )
| A. | ${y^2}=2\sqrt{6}x$ | B. | ${y^2}=4\sqrt{6}x$ | C. | ${x^2}=2\sqrt{6}y$ | D. | ${x^2}=4\sqrt{6}y$ |
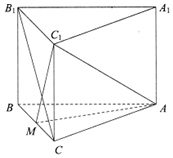 在三棱柱ABC-A1B1C1中,已知侧棱CC1⊥底面ABC,M为BC的中点,$AC=AB=3,BC=2,C{C_1}=\sqrt{2}$.
在三棱柱ABC-A1B1C1中,已知侧棱CC1⊥底面ABC,M为BC的中点,$AC=AB=3,BC=2,C{C_1}=\sqrt{2}$.