题目内容
9. 已知函数$f(x)=\left\{\begin{array}{l}x+2{\;}^{\;}(x<0)\\{x^2}{\;}^{\;}{\;}^{\;}(0≤x<2)\\ \frac{1}{2}x{\;}^{\;}{\;}^{\;}(x≥2)\end{array}\right.$
已知函数$f(x)=\left\{\begin{array}{l}x+2{\;}^{\;}(x<0)\\{x^2}{\;}^{\;}{\;}^{\;}(0≤x<2)\\ \frac{1}{2}x{\;}^{\;}{\;}^{\;}(x≥2)\end{array}\right.$(1)求f(f(f(-$\frac{1}{2}$)))的值;
(2)若f(a)=2,求a的值.
(3)画出此函数的图象.
分析 (1)由分段函数的解析式,分别计算f(-$\frac{1}{2}$)=2-$\frac{1}{2}$=$\frac{3}{2}$,f($\frac{3}{2}$)=$\frac{9}{4}$,f($\frac{9}{4}$)=$\frac{9}{8}$.即可得到所求值;
(2)对a讨论,分别运用f(x)的三段解析式,解方程可得a的值;
(3)运用分段函数的图象画法,可得图象.
解答  解:(1)函数$f(x)=\left\{\begin{array}{l}x+2{\;}^{\;}(x<0)\\{x^2}{\;}^{\;}{\;}^{\;}(0≤x<2)\\ \frac{1}{2}x{\;}^{\;}{\;}^{\;}(x≥2)\end{array}\right.$,
解:(1)函数$f(x)=\left\{\begin{array}{l}x+2{\;}^{\;}(x<0)\\{x^2}{\;}^{\;}{\;}^{\;}(0≤x<2)\\ \frac{1}{2}x{\;}^{\;}{\;}^{\;}(x≥2)\end{array}\right.$,
可得f(-$\frac{1}{2}$)=2-$\frac{1}{2}$=$\frac{3}{2}$,f($\frac{3}{2}$)=$\frac{9}{4}$,f($\frac{9}{4}$)=$\frac{9}{8}$.
则f(f(f(-$\frac{1}{2}$)))=$\frac{9}{8}$;
(2)若f(a)=2,当a<0时,a+2=2,解得a=0不成立;
当0≤a<2,a2=2,解得a=$\sqrt{2}$(-$\sqrt{2}$舍去);
当a≥2时,$\frac{1}{2}$a=2,解得a=4.
故$a=\sqrt{2}或4$;
(3)由分段函数的图象画法可得,
如图所示:
点评 本题考查分段函数的图象和应用:求函数值和自变量的值,考查运算能力,属于基础题.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
14.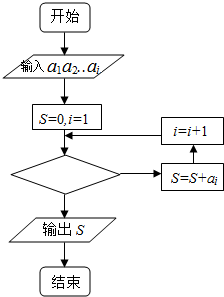 某篮球队6名主力队员在最近三场比赛中投进的三分球个数如表所示:
某篮球队6名主力队员在最近三场比赛中投进的三分球个数如表所示:
如图是统计该6名队员在最近三场比赛中投进的三分球总数的程序框图,则图中判断框应填i<7(或i≤6),输出的s=51.
 某篮球队6名主力队员在最近三场比赛中投进的三分球个数如表所示:
某篮球队6名主力队员在最近三场比赛中投进的三分球个数如表所示:| 队员i | 1 | 2 | 3 | 4 | 5 | 6 |
| 三分球个数ai | 9 | 13 | 11 | 7 | 5 | 6 |