题目内容
11.已知等比数列{an}的公比q>1,且2(an+an+2)=5an+1,n∈N*.(Ⅰ)求q的值;
(Ⅱ)若a52=a10,求数列{$\frac{{a}_{n}}{{3}^{n}}$}的前n项和Sn.
分析 (I)利用等比数列的通项公式即可得出;
(II)利用等比数列的通项公式及其前n项和公式即可得出.
解答 解:(I)∵2(an+an+2)=5an+1,n∈N*,∴$2{a}_{n}(1+{q}^{2})$=5anq,
化为2(1+q2)=5q,又q>1,
解得q=2.
(II)a52=a10,$({a}_{1}×{2}^{4})^{2}$=a1×29,解得a1=2.
∴an=2n.
∴$\frac{{a}_{n}}{{3}^{n}}$=$(\frac{2}{3})^{n}$.
∴数列{$\frac{{a}_{n}}{{3}^{n}}$}的前n项和Sn=$\frac{\frac{2}{3}[1-(\frac{2}{3})^{n}]}{1-\frac{2}{3}}$=$2[1-(\frac{2}{3})^{n}]$.
点评 本题考查了等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
3.函数f(x)=4x2-mx+5在区间(-∞,-2)上是递减,在区间[-2,+∞)上递增,则f(1)=( )
| A. | -7 | B. | 1 | C. | 17 | D. | 25 |
19.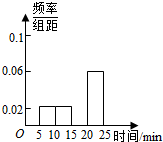 某车站在春运期间为了改进服务,随机抽样调查了100名旅客从开始在购票窗口排队到购到车票所用的时间t(以下简称购票用时,单位:min).下面是这次抽样的频率分布表和频率分布直方图,解答下列问题:
某车站在春运期间为了改进服务,随机抽样调查了100名旅客从开始在购票窗口排队到购到车票所用的时间t(以下简称购票用时,单位:min).下面是这次抽样的频率分布表和频率分布直方图,解答下列问题:
(1)这次抽样的样本容量是多少?
(2)在表中填写缺失的数据并补全频率分布直方图.
(3)求旅客购票用时的平均数
(4)若每增加一个购票窗口可使平均购票用时缩短5min,要使平均购票用时不超过10min,那么你估计最少要增加几个窗口?
 某车站在春运期间为了改进服务,随机抽样调查了100名旅客从开始在购票窗口排队到购到车票所用的时间t(以下简称购票用时,单位:min).下面是这次抽样的频率分布表和频率分布直方图,解答下列问题:
某车站在春运期间为了改进服务,随机抽样调查了100名旅客从开始在购票窗口排队到购到车票所用的时间t(以下简称购票用时,单位:min).下面是这次抽样的频率分布表和频率分布直方图,解答下列问题:| 分组 | 频数 | 频率 | |
| 一组 | 0≤t<5 | 0 | 0 |
| 二组 | 5≤t<10 | 10 | 0.10 |
| 三组 | 10≤t<15 | 10 | 0.10 |
| 四组 | 15≤t<20 | 50 | 0.50 |
| 五组 | 20≤t<25 | 30 | 0.30 |
| 合计 | 100 | 1.00 | |
(2)在表中填写缺失的数据并补全频率分布直方图.
(3)求旅客购票用时的平均数
(4)若每增加一个购票窗口可使平均购票用时缩短5min,要使平均购票用时不超过10min,那么你估计最少要增加几个窗口?
6.已知m,n为空间中两条不同的直线,α,β为空间中两个不同的平面,下列命题中正确的是( )
| A. | 若m∥α,m∥β,则α∥β | B. | 若m⊥α,m⊥n,则n∥α | C. | 若m∥α,m∥n,则n∥α | D. | 若m⊥α,m∥β,则α⊥β |
19.已知一平面图形的斜二侧画法的水平放置的直观图如图所示,则原来图形的面积为( )
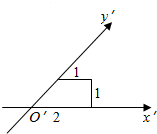

| A. | $\frac{3}{2}$ | B. | 3 | C. | $3\sqrt{2}$ | D. | $6\sqrt{2}$ |