题目内容
20.已知函数f(x)=log2(x+1)的定义域为集合A,集合B={x|ax-1<0,a∈N*},集合C={y|y=$(\frac{1}{2})^{x+2}}$,x∈A}.(1)求集合C;
(2)若C?(A∩B),求a的值.
分析 (1)由f(x)=log2(x+1)的定义域为集合A,求出A的集合,由集合B={x|ax-1<0,a∈N*},求出B的集合,然后再由指数函数的性质求出集合C.
(2)由集合A,集合B求出A∩B,再由C?(A∩B),即可得到a的值.
解答 解:由函数f(x)=log2(x+1)的定义域为集合A,得A=(-1,+∞),集合B={x|ax-1<0,a∈N*}={x|$x<\frac{1}{a}$},
(1)集合C={y|y=$(\frac{1}{2})^{x+2}}$,x∈A},$y={({\frac{1}{2}})^{x+2}}$在(-1,+∞)上单调递减,则$y∈({0,\frac{1}{2}})$,则 C=$({0,\frac{1}{2}})$;
(2)由于a∈N*,B=$({-∞,\frac{1}{a}})$,
则$A∩B=({-1,\frac{1}{a}})$,由C?(A∩B),得$\frac{1}{a}≥\frac{1}{2}$⇒a≤2.
即a=1或2.
点评 本题考查了交、并、补集的混合运算,考查了集合的包含关系判断及应用,是基础题.

练习册系列答案
相关题目
11.设A(2,3,-6),B(6,4,4),C(3,7,4)是平行四边形ABCD的三个顶点,则这个平行四边形的面积为( )
| A. | $\frac{5\sqrt{26}}{26}$ | B. | 45 | C. | 3$\sqrt{2}$ | D. | $\frac{45}{2}$ |
15.已知函数f(x)=a-$\frac{1}{{{2^x}+1}}$.
(1)若f(x)为奇函数,求a的值;
(2)证明:不论a为何值f(x)在R上都单调递增;
(3)在(1)的条件下,求f(x)的值域.
(1)若f(x)为奇函数,求a的值;
(2)证明:不论a为何值f(x)在R上都单调递增;
(3)在(1)的条件下,求f(x)的值域.
4.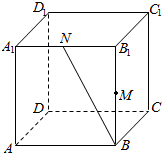 棱长为1的正方体ABCD-A1B1C1D1中,M,N分别是A1B1,BB1的中点,点P在正方体的表面上运动,则总能使MP⊥BN的点P所形成图形的周长是( )
棱长为1的正方体ABCD-A1B1C1D1中,M,N分别是A1B1,BB1的中点,点P在正方体的表面上运动,则总能使MP⊥BN的点P所形成图形的周长是( )
 棱长为1的正方体ABCD-A1B1C1D1中,M,N分别是A1B1,BB1的中点,点P在正方体的表面上运动,则总能使MP⊥BN的点P所形成图形的周长是( )
棱长为1的正方体ABCD-A1B1C1D1中,M,N分别是A1B1,BB1的中点,点P在正方体的表面上运动,则总能使MP⊥BN的点P所形成图形的周长是( )| A. | 4 | B. | $2+\sqrt{2}$ | C. | $3+\sqrt{5}$ | D. | $2+\sqrt{5}$ |