题目内容
13.设曲线y=ax2在点x=1处的切线与直线2x-y+b=0平行,则a=( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $-\frac{1}{2}$ | D. | -1 |
分析 求出函数的导数,利用导数的几何意义建立方程关系进行求解即可.
解答 解:∵y=ax2,
∴y′=f′(x)=2ax,
则f′(1)=2a,即曲线y=ax2在点x=1处的切线斜率k=f′(1)=2a,
直线2x-y+b=0平行得斜率k=2,
∵y=ax2在点x=1处的切线与直线2x-y+b=0平行,
∴2a=2,即a=1,
故选:A.
点评 本题主要考查导数的几何意义的应用,根据直线平行建立直线斜率相等的关系是解决本题的关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
18.如图,点A,B,C是圆O上的点,且AB=2,BC=$\sqrt{6}$,∠CAB=120°,则∠AOB对应的劣弧长为( )
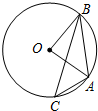

| A. | π | B. | $\frac{π}{3}$ | C. | $\frac{{\sqrt{2}}}{2}π$ | D. | $\frac{π}{2}$ |
5.若方程(m-1)x2+(3-m)y2=(m-1)(3-m)表示焦点在y轴上的椭圆,则实数m的取值范围是( )
| A. | (-∞,1) | B. | (1,2) | C. | (2,3) | D. | (3,+∞) |
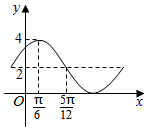 已知函数f(x)=Asin(ωx+φ)+B(A>0,ω,0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(π)的值为3.
已知函数f(x)=Asin(ωx+φ)+B(A>0,ω,0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(π)的值为3. 如图所示,O是正三角形ABC的中心,四边形AOBE和AOCD均为平行四边形,则与向量$\overrightarrow{AD}$相等的向量有$\overrightarrow{OC}$;与向量$\overrightarrow{OA}$共线的向量有$\overrightarrow{DC}$和$\overrightarrow{EB}$;与向量$\overrightarrow{OA}$的模相等的向量有$\overrightarrow{OB}$、$\overrightarrow{OC}$、$\overrightarrow{AE}$、$\overrightarrow{AD}$、$\overrightarrow{DC}$和$\overrightarrow{EB}$(填图中所画的向量)
如图所示,O是正三角形ABC的中心,四边形AOBE和AOCD均为平行四边形,则与向量$\overrightarrow{AD}$相等的向量有$\overrightarrow{OC}$;与向量$\overrightarrow{OA}$共线的向量有$\overrightarrow{DC}$和$\overrightarrow{EB}$;与向量$\overrightarrow{OA}$的模相等的向量有$\overrightarrow{OB}$、$\overrightarrow{OC}$、$\overrightarrow{AE}$、$\overrightarrow{AD}$、$\overrightarrow{DC}$和$\overrightarrow{EB}$(填图中所画的向量)