题目内容
3.定义在R上的奇函数f(x),当x≥0时,f(x)=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{3}}(x+1),x∈[0,2]}\\{1-|x-4|,x∈[2,+∞)}\end{array}\right.$,则关于x的函数F(x)=f(x)-a(0<a<1)的所有零点之和为1-3a.分析 作函数f(x)与y=a的图象,从而可得函数F(x)=f(x)-a有5个零点,设5个零点分别为b<c<d<e<f,从而结合图象解得.
解答 解:作函数f(x)与y=a的图象如下, ,
,
结合图象可知,
函数f(x)与y=a的图象共有5个交点,
故函数F(x)=f(x)-a有5个零点,
设5个零点分别为b<c<d<e<f,
∴b+c=2×(-4)=-8,e+f=2×4=8,
-$lo{g}_{\frac{1}{3}}$(-x+1)=a,
故x=1-3a,即d=1-3a,
故b+c+d+e+f=1-3a,
故答案为:1-3a.
点评 本题考查了函数的零点与函数的图象的关系应用及数形结合的思想应用.

练习册系列答案
相关题目
11.当-$\frac{π}{2}$≤x≤$\frac{π}{2}$时,函数f(x)=2sin(x+$\frac{π}{3}$)有( )
| A. | 最大值1,最小值-1 | B. | 最大值1,最小值-$\frac{1}{2}$ | ||
| C. | 最大值2,最小值-2 | D. | 最大值2,最小值-1 |
11.球O半径为R=13,球面上有三点A、B、C,AB=12$\sqrt{3}$,AC=BC=12,则四面体OABC的体积是( )
| A. | 60$\sqrt{3}$ | B. | 50$\sqrt{3}$ | C. | 60$\sqrt{6}$ | D. | 50$\sqrt{6}$ |
18.已知f(x)=2x+1,则f(2)=( )
| A. | 5 | B. | 0 | C. | 1 | D. | 2 |
8.直线x=1的倾斜角是( )
| A. | 0 | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | 不存在 |
13.设曲线y=ax2在点x=1处的切线与直线2x-y+b=0平行,则a=( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $-\frac{1}{2}$ | D. | -1 |
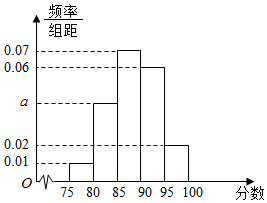 某地区有100名学员参加交通法规考试,考试成绩的频率分布直方图如图所示.其中成绩分组区间是:第1组:[75,80),第2组:[80,85),第3组:[85,90),第4组:[90,95),第5组:[95,100].
某地区有100名学员参加交通法规考试,考试成绩的频率分布直方图如图所示.其中成绩分组区间是:第1组:[75,80),第2组:[80,85),第3组:[85,90),第4组:[90,95),第5组:[95,100].