题目内容
2.已知函数f(x)=sin2x-sin2(x-$\frac{π}{6}$),x∈R.(1)求f(x)的单调区间.
(2)若关于x的方程2f(x)-m+1=0在区间[-$\frac{π}{3}$,$\frac{π}{4}$]上有两个相异的实根,求m的取值范围.
分析 (1)由条件利用三角恒等变换化简函数的解析式,再利用正弦函数的单调性求得f(x)的单调减区间.
(2)由题意可知,函数y=2f(x)与函数y=m-1的图象在区间$[-\frac{π}{3},\frac{π}{4}]$上有两个交点,结合图象求得m的范围.
解答 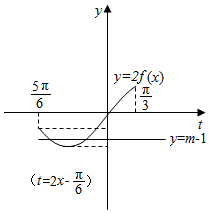 解:( 1 ) 由已知,有f(x)=$\frac{1-cos2x}{2}-\frac{{1-cos({2x-\frac{π}{3}})}}{2}=\frac{1}{2}({\frac{1}{2}cos2x+\frac{{\sqrt{3}}}{2}sin2x})-\frac{1}{2}$cos2x
解:( 1 ) 由已知,有f(x)=$\frac{1-cos2x}{2}-\frac{{1-cos({2x-\frac{π}{3}})}}{2}=\frac{1}{2}({\frac{1}{2}cos2x+\frac{{\sqrt{3}}}{2}sin2x})-\frac{1}{2}$cos2x
=$\frac{{\sqrt{3}}}{4}sin2x-\frac{1}{4}cos2x=\frac{1}{2}sin({2x-\frac{π}{6}})$.
设2kπ+$\frac{π}{2}≤2x-\frac{π}{6}≤2kπ+\frac{3π}{2}$,解得kπ+$\frac{π}{3}≤x≤kπ+\frac{5π}{6}$,
故f(x)的单调减区间为:$[kπ+\frac{π}{3}\;,\;kπ+\frac{5π}{6}]\;\;(k∈Z)$.
(2)由题意可知,函数y=2f(x)与函数y=m-1的图象在
区间$[-\frac{π}{3},\frac{π}{4}]$上有两个交点,
∵$x∈[-\frac{π}{3},\frac{π}{4}]\;\;∴2x-\frac{π}{6}∈[-\frac{5π}{6},\frac{π}{3}]$,
∴2f(x)=2•$\frac{1}{2}$sin(2x-$\frac{π}{6}$)∈[-1,$\frac{\sqrt{3}}{2}$],
结合图象可得:-1<m-1≤-$\frac{1}{2}$,解得0<m≤$\frac{1}{2}$.
点评 本题主要考查三角恒等变换,正弦函数的单调性,正弦函数的图象特征,属于中档题.

| A. | 1 | B. | $\frac{1}{2}$ | C. | $-\frac{1}{2}$ | D. | -1 |
| A. | 2 | B. | -2 | C. | 5 | D. | -5 |
| 井号I | 1 | 2 | 3 | 4 | 5 | 6 |
| 坐标(x,y)(km) | (2,30) | (4,40) | (5,60) | (6,50) | (8,70) | (1,y) |
| 钻探深度(km) | 2 | 4 | 5 | 6 | 8 | 10 |
| 出油量(L) | 40 | 70 | 110 | 90 | 160 | 205 |
(Ⅱ)现准备勘探新井7(1,25),若通过1、3、5、7号井计算出的$\widehatb,\widehata$的值与(I)中b,a的值差不超过10%,则使用位置最迫近的已有旧井6(1,y),否则在新位置打开,请判断可否使用旧井?($\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n_x^{-2}}}},\widehata=\overline y-\widehatb\overline x,\sum_{i=1}^4{{x_{2i-1}}^2=94,\sum_{i=1}^4{{x_{2i-1}}{y_{2i-1}}=945}}$)
(Ⅲ)设口井出油量与勘探深度的比值k不低于20的勘探并称为优质井,那么在原有6口井中任意勘探4口井,求勘探优质井数X的分布列与数学期望.