题目内容
9. 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥底面ABCD,M是棱PD的中点,且PA=AB=AC=2,BC=2$\sqrt{2}$.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥底面ABCD,M是棱PD的中点,且PA=AB=AC=2,BC=2$\sqrt{2}$.(Ⅰ)求证:CD⊥平面PAC;
(Ⅱ)N是棱AB上一点,且三棱锥A-MNC的体积等于四棱锥P-ABCD体积的$\frac{1}{12}$,求$\frac{AN}{NB}$的值.
分析 (1)由PA⊥平面ABCD得PA⊥CD,由勾股定理的逆定理得AC⊥BC,故CD⊥平面PAC.
(2)设AN=x,求出三棱锥A-MNC和四棱锥P-ABCD的体积,利用体积比得出x,从而求出$\frac{AN}{NB}$的值.
解答 (1)证明:∵AB=AC=2,BC=2$\sqrt{2}$,
∴AB2+AC2=BC2,∴AB⊥AC.
∵底面ABCD是平行四边形,
∴AB∥CD,∴AC⊥CD.
∵PA⊥平面ABCD,CD?平面ABCD,
∴PA⊥CD,又PA∩AC=A,PA?平面PAC,AC?平面PAC,
∴CD⊥平面PAC.
(2)解:设AN=x,则S△ANC=$\frac{1}{2}AN•AC=x$,
∵M是PD的中点,∴M到平面ABCD的距离h=$\frac{1}{2}PA$=1.
∴V=A-MNC=VM-ANC=$\frac{1}{3}{S}_{△ANC}•h$=$\frac{x}{3}$.
∵VP-ABCD=$\frac{1}{3}{S}_{四边形ABCD}•PA$=$\frac{1}{3}×2×2×2$=$\frac{8}{3}$.
∵三棱锥A-MNC的体积等于四棱锥P-ABCD体积的$\frac{1}{12}$,
∴$\frac{x}{3}=\frac{8}{3}×\frac{1}{12}$,∴x=$\frac{2}{3}$.即AN=$\frac{2}{3}$.
∴BN=AB-AN=$\frac{4}{3}$.
∴$\frac{AN}{NB}=\frac{1}{2}$.
点评 本题考查了线面垂直的判定,棱锥的体积计算,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.若直线l过点P(-3,-$\frac{3}{2}$)且被圆x2+y2=25截得的弦长是8,则直线l的方程为( )
| A. | 3x+4y+15=0 | B. | x=-3或3x+4y+15=0 | ||
| C. | x=-3或y=-$\frac{3}{2}$ | D. | x=-3 |
14.一底面是直角梯形的四棱柱的正(主)视图,侧(左)视图如图所示,则该四棱柱的体积为( )
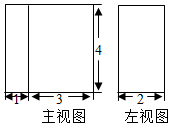

| A. | 20 | B. | 28 | C. | 20或32 | D. | 20或28 |
19.已知命题:“若abc=0,则实数a,b,c中至少有一个为0”,用反证法证明该命题时的假设为( )
| A. | 假设a,b,c都不为0 | B. | 假设a,b,c中至少有两个为0 | ||
| C. | 假设a,b,c中至多有两个为0 | D. | 假设a,b,c中至多有一个为0 |
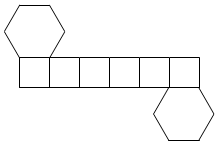 已知一个凸多边形的平面展开图由两个正六边形和六个正方形构成,如图所示,若该凸多面体所有棱长均为1,则其体积V=$\frac{3\sqrt{3}}{2}$.
已知一个凸多边形的平面展开图由两个正六边形和六个正方形构成,如图所示,若该凸多面体所有棱长均为1,则其体积V=$\frac{3\sqrt{3}}{2}$.