题目内容
已知函数f(x)=2
sin2(
+x)-
(cos2x+1)(x∈R).
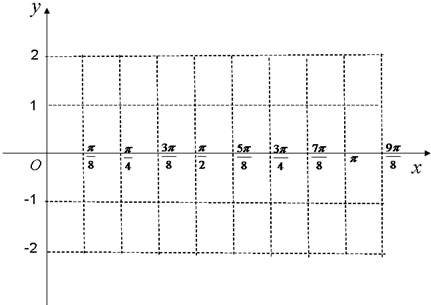
(1)用“五点法”作出函数f(x)在区间[
,
]上的简图;
(2)当x∈(
,
)时,恒有-3<f(x)-m<3成立,求实数m的取值范围.
| 2 |
| π |
| 4 |
| 2 |

(1)用“五点法”作出函数f(x)在区间[
| π |
| 8 |
| 9π |
| 8 |
(2)当x∈(
| π |
| 4 |
| π |
| 2 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,三角函数中的恒等变换应用
专题:三角函数的图像与性质
分析:(1)化简可得f(x)=2sin(2x-
),列表描点可得图象,
(2)由x的范围可得f(x)的范围,问题于x∈(
,
)时,m-3<f(x)<m+3,由恒成立可得m的不等式组,解不等式组可得.
| π |
| 4 |
(2)由x的范围可得f(x)的范围,问题于x∈(
| π |
| 4 |
| π |
| 2 |
解答:
解:化简可得f(x)=2
sin2(
+x)-
(cos2x+1)
=2
×
-
cos2x-
=
sin2x-
cos2x=2sin(2x-
)
(1)列表:

(2)由x∈(
,
)可得
<2x-
<
,
∴
<2sin(2x-
)≤2,
∴当x∈(
,
)时,恒有-3<f(x)-m<3成立,
等价于x∈(
,
)时,m-3<f(x)<m+3,
∴
,解得-1<m≤3+
.
| 2 |
| π |
| 4 |
| 2 |
=2
| 2 |
1-cos(
| ||
| 2 |
| 2 |
| 2 |
=
| 2 |
| 2 |
| π |
| 4 |
(1)列表:
| x |
|
|
|
|
| ||||||||||
2x-
|
0 |
|
π |
|
2π | ||||||||||
| f(x) | 0 | 2 | 0 | -2 | 0 |

(2)由x∈(
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
∴
| 2 |
| π |
| 4 |
∴当x∈(
| π |
| 4 |
| π |
| 2 |
等价于x∈(
| π |
| 4 |
| π |
| 2 |
∴
|
| 2 |
点评:本题考查三角函数的图象和性质,涉及三角函数公式的应用,属中档题.

练习册系列答案
相关题目
离散型随机变量的分布列为:
则x的值为( )
| ξ | 0 | 1 | 2 | 3 | ||||||
| P |
|
|
|
x |
A、
| ||
B、
| ||
C、
| ||
D、
|

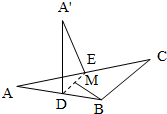 在直角△ABC中,AB=BC=2,D,E分别是AB,AC的中点,将△ADE沿线段DE折起到△A′DE,使平面A′DE⊥平面DBCE,当M是DE的中点时,证明:BM⊥面A′CD.
在直角△ABC中,AB=BC=2,D,E分别是AB,AC的中点,将△ADE沿线段DE折起到△A′DE,使平面A′DE⊥平面DBCE,当M是DE的中点时,证明:BM⊥面A′CD.