题目内容
若x>0,y>0,x+y=1,则
+
有最小值 .
| 1 |
| y |
| 2 |
| x |
考点:基本不等式
专题:不等式的解法及应用
分析:转化为,(x+y)(
+
)=
+
+3,利用基本不等式求解即可.
| 1 |
| y |
| 2 |
| x |
| x |
| y |
| 2y |
| x |
解答:
解:∵>0,y>0,x+y=1,
∴
+
,x>0,y>0,(x+y)(
+
)=
+
+3≥2
+3,(x2=2y2等号成立,即x=2-
,x=2
-2)
∴
+
有最小值为:2
+3,
故答案为:2
+3
∴
| 1 |
| y |
| 2 |
| x |
| 1 |
| y |
| 2 |
| x |
| x |
| y |
| 2y |
| x |
| 2 |
| 2 |
| 2 |
∴
| 1 |
| y |
| 2 |
| x |
| 2 |
故答案为:2
| 2 |
点评:本题考查了基本不等式在求解二元代数式的最值的运用,属于中档题,注意等号成立的条件.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
已知奇函数f(x)为R上的减函数,则关于a的不等式f(a2)+f(2a)>0的解集是( )
| A、(-2,0 ) |
| B、( 0,2 ) |
| C、(-2,0 )∪( 0,2 ) |
| D、(-∞,-2 )∪( 0,+∞) |
已知集合A={x|x(x-1)≤0,x∈R},B={x|-2<x<1,x∈R},那么集合A∩B是( )
| A、{x|-2<x≤1,x∈R} |
| B、{x|0≤x<1,x∈R} |
| C、{x|0<x≤1,x∈R} |
| D、{x|0<x<1,x∈R} |
已知函数f(x)=
,则f(f(1))=( )
|
| A、4 | B、5 | C、28 | D、19 |
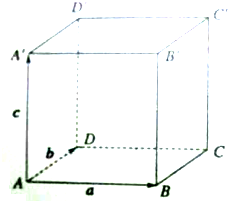 已知正方体ABCD-A′B′C′D′的棱长为1,设
已知正方体ABCD-A′B′C′D′的棱长为1,设