题目内容
5.关于函数f(x)=2cos2$\frac{x}{2}$+$\sqrt{3}$sinx(x∈[0,π])下列结论正确的是( )| A. | 有最大值3,最小值-1 | B. | 有最大值2,最小值-2 | ||
| C. | 有最大值3,最小值0 | D. | 有最大值2,最小值0 |
分析 利用二倍角和辅助角公式基本公式将函数化为y=Asin(ωx+φ)的形式,x∈[0,π]时,求出内层函数的取值范围,结合三角函数的图象和性质,求出f(x)的最大值和最小值.
解答 解:函数f(x)=2cos2$\frac{x}{2}$+$\sqrt{3}$sinx.
化简可得:f(x)=cosx+$\sqrt{3}$sinx+1=2sin(x+$\frac{π}{6}$)+1
∵x∈[0,π],
∴x+$\frac{π}{6}$∈[$\frac{π}{6}$,$\frac{7π}{6}$],
可得sin(x+$\frac{π}{6}$)∈[$-\frac{1}{2}$,1]
∴函数f(x)∈[0,3],
故选:C.
点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用,利用三角函数公式将函数进行化简是解决本题的关键,属于基础题.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
13.已知F1,F2分别是双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1的左、右焦点,若点F2关于直线bx-ay=0的对称点恰好落在以F1为圆心,|OF1|为半径的圆上,则双曲线C的离心率为( )
| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 3 |
20.5位大学毕业生分配到3家单位,每家单位至少录用1人,则不同的分配方法共有( )
| A. | 25种 | B. | 60种 | C. | 90种 | D. | 150种 |
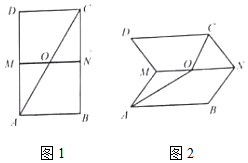 如图1,2,已知ABCD是矩形,M,N分别为边AD,BC的中点,MN与AC交于点O,沿MN将矩形MNCD折起,设AB=2,BC=4,二面角B-MN-C的大小为θ.
如图1,2,已知ABCD是矩形,M,N分别为边AD,BC的中点,MN与AC交于点O,沿MN将矩形MNCD折起,设AB=2,BC=4,二面角B-MN-C的大小为θ.