题目内容
7.已知函数f(x)=|x+1|-a|x-l|.(Ⅰ)当a=-2时,解不等式f(x)>5;
(Ⅱ)若(x)≤a|x+3|,求a的最小值.
分析 (Ⅰ)将a=2代入f(x),表示出f(x)的分段形式,结合函数的单调性求出不等式的解集即可;(Ⅱ)问题转化为$\frac{|x+1|}{|x-1|+|x+3|}$≤$\frac{1}{2}$,求出a的最小值即可.
解答 解:(Ⅰ)当a=-2时,f(x)=$\left\{\begin{array}{l}{1-3x,x<-1}\\{3-x,-1≤x≤1}\\{3x-1,x>1}\end{array}\right.$,
由f(x)的单调性及f(-$\frac{4}{3}$)=f(2)=5,
得f(x)>5的解集为{x|x<-$\frac{4}{3}$,或x>2}.…(5分)
(Ⅱ)由f(x)≤a|x+3|得a≥$\frac{|x+1|}{|x-1|+|x+3|}$,
由|x-1|+|x+3|≥2|x+1|得$\frac{|x+1|}{|x-1|+|x+3|}$≤$\frac{1}{2}$,得a≥$\frac{1}{2}$.
(当且仅当x≥1或x≤-3时等号成立)
故a的最小值为$\frac{1}{2}$.…(10分)
点评 本题考查了解绝对值不等式问题,考查分段函数,是一道中档题.

练习册系列答案
相关题目
20.在等差数列中,am=n,an=m(m≠n),则am+n为( )
| A. | m-n | B. | 0 | C. | m2 | D. | n2 |
18.设x,y满足约束条件$\left\{\begin{array}{l}{x+y-2≥0}\\{x-y+2≥0}\\{x≤2}\end{array}\right.$,则目标函数z=$\frac{y}{x+1}$的取值范围是( )
| A. | [-2,0] | B. | (-∞,-2]∪[0,+∞) | C. | [0,2] | D. | (-∞,0]∪[2,+∞) |
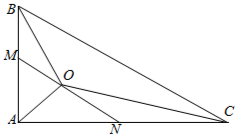 如图所示,△ABC中,AB⊥AC,AB=6,AC=8.边AB,AC的中点分别为M,N.若O为线段MN上任一点,则$\overrightarrow{OB}•\overrightarrow{OC}+\overrightarrow{OA}•\overrightarrow{OB}+\overrightarrow{OA}•\overrightarrow{OC}$的取值范围是[$-\frac{180}{11},-9$].
如图所示,△ABC中,AB⊥AC,AB=6,AC=8.边AB,AC的中点分别为M,N.若O为线段MN上任一点,则$\overrightarrow{OB}•\overrightarrow{OC}+\overrightarrow{OA}•\overrightarrow{OB}+\overrightarrow{OA}•\overrightarrow{OC}$的取值范围是[$-\frac{180}{11},-9$].