题目内容
给出下列结论,其中错误的是( )
| A、若命题p:?x0∈R,x02+x0+1<0,则¬p:?x∈R,x2+x+1≥0 |
| B、?x∈R,2x>x2 |
| C、“若am2≤bm2,则a<b”是假命题 |
| D、“a>1,b>1”是“ab>1”的充分条件 |
考点:复合命题的真假,全称命题,特称命题,命题的否定,必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据特称命题的否定,找反例的方法,以及同向正的不等式相乘即可判断每个选项的正误,找出正确选项.
解答:
解:A.根据特称命题的否定是全称命题知A正确;
B.x=3时,23<32,∴B错误;
C.若am2≤bm2,当m2=0时a,b取任意值,即得不到a<b,∴该命题是假命题,即C正确;
D.a>1,b>1时,能得到ab>1,所以“a>1,b>1”是“ab>1”的充分条件,即D正确;
∴结论错误的是B.
故选B.
B.x=3时,23<32,∴B错误;
C.若am2≤bm2,当m2=0时a,b取任意值,即得不到a<b,∴该命题是假命题,即C正确;
D.a>1,b>1时,能得到ab>1,所以“a>1,b>1”是“ab>1”的充分条件,即D正确;
∴结论错误的是B.
故选B.
点评:考查特称命题的否定是全称命题,以及举反例说明结论不成立的方法,充分条件的概念.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知f(x)的图象如图所示,则下列数值按从小到大的排列顺序正确的是( )
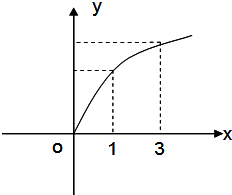

A、f′(1),f′(3),f(0),
| ||
B、f(0),f′(3),
| ||
C、
| ||
D、f(0),
|
不等式|4-3x|-5≤0的解集是( )
A、{x|-
| ||
B、{x|x≤-
| ||
C、{x|
| ||
D、{x|-
|
直线λx+y+λ-2=0不过第三象限,则λ的取值范围是( )
| A、[0,1] |
| B、[0,2] |
| C、(-∞,4] |
| D、[4,+∞) |
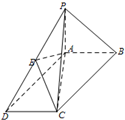 如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点.
如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点.