题目内容
8．
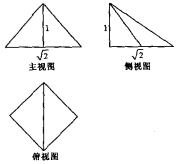刘徽的《九章算术注》中有这样的记载：“邪解立方有两堑堵，邪解堑堵，其一为阳马，一为鳖臑，阳马居二，鳖臑居一，不易之率也．”意思是说：把一块立方体沿斜线分成相同的两块，这两块叫做堑堵，再把一块堑堵沿斜线分成两块，大的叫阳马，小的叫鳖臑，两者体积比为2：1，这个比率是不变的，如图是一个阳马的三视图，则其表面积为（ ）| A． | 2 | B． | 2+$\sqrt{2}$ | C． | 3+$\sqrt{3}$ | D． | 3+$\sqrt{2}$ |
分析 根据几何体的三视图知该几何体是底面为正方形，
且一侧棱垂直于底面的四棱锥，结合图形求出它的表面积．
解答 
解：根据几何体的三视图知，该几何体是底面为正方形，
且一侧棱垂直于底面的四棱锥，如图所示；
根据图中数据，计算其表面积为
S=S正方形ABCD+S△PAB+S△PBC+S△PCD+S△PAD
=12+$\frac{1}{2}$×1×1+$\frac{1}{2}$×1×$\sqrt{2}$+$\frac{1}{2}$×1×$\sqrt{2}$+$\frac{1}{2}$×1×1
=2+$\sqrt{2}$．
故选：B．
点评 本题考查了几何体三视图的应用问题，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
在图所示的几何体中，底面ABCD为正方形，PD⊥平面ABCD，EC∥PD，且PD=AD=2EC=2，N为线段PB的中点．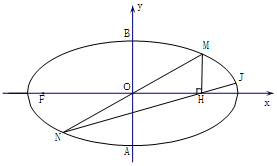
已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左焦点为F，短轴的两个端点分别为A、B，且|AB|=2，△ABF为等边三角形．