题目内容
3.在△ABC中,设内角A,B,C所对边分别为a,b,c,且sin(A-$\frac{π}{6}$)-cos(A+$\frac{5π}{3}$)=$\frac{\sqrt{2}}{2}$.(1)求角A的大小;
(2)若a=$\sqrt{5}$,sin2B+cos2C=1,求b,c.
分析 (1)由诱导公式、两角差的正弦、余弦函数化简已知的等式,由内角的范围和特殊角的三角函数值求出角A的大小;
(2)由二倍角余弦公式的变形化简sin2B+cos2C=1,由正弦定理化简后,由条件和余弦定理列出方程求出b,c的值.
解答 解:(1)因为sin(A-$\frac{π}{6}$)-cos(A+$\frac{5π}{3}$)=$\frac{\sqrt{2}}{2}$,
所以sin(A-$\frac{π}{6}$)-cos(A-$\frac{π}{3}$)=$\frac{\sqrt{2}}{2}$,
则$\frac{\sqrt{3}}{2}$sinA-$\frac{1}{2}$cosA-($\frac{1}{2}$cosA+$\frac{\sqrt{3}}{2}$sinA)=$\frac{\sqrt{2}}{2}$,
化简得cosA=$-\frac{\sqrt{2}}{2}$,
又0<A<π,则A=$\frac{3π}{4}$;
(2)因为sin2B+cos2C=1,所以sin2B+1-2sin2C=1,
即sin2B=2sin2C,
由正弦定理得,b2=2c2,则b=$\sqrt{2}$c,
又a=$\sqrt{5}$,由余弦定理得,a2=b2+c2-2bccosA,
则5=2c2+c2-2$\sqrt{2}$c2×$(-\frac{\sqrt{2}}{2})$,解得c=1,
则b=$\sqrt{2}$c=$\sqrt{2}$.
点评 本题考查正弦定理、余弦定理,诱导公式,两角差的正弦、余弦函数,以及二倍角余弦公式的变形的应用,考查转化思想、方程思想,化简、变形能力.

练习册系列答案
相关题目
14.某人的身份证号码是340304199803041290,随机掷一枚骰子,出现的点数是身份证上的数字的概率为( )
| A. | $\frac{2}{9}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{6}$ |
11.某工厂拟生产甲、乙两种实销产品.已知每件甲产品的利润为0.4万元,每件乙产品的利润为0.3万元,两种产品都需要在A,B两种设备上加工,且加工一件甲、乙产品在A,B设备上所需工时(单位:h)分别如表所示.
若A设备每月的工时限额为400h,B设备每月的工时限额为300h,则该厂每月生产甲、乙两种产品可获得的最大利润为( )
| 甲产品所需工时 | 乙产品所需工时 | |
| A设备 | 2 | 3 |
| B设备 | 4 | 1 |
| A. | 40万元 | B. | 45万元 | C. | 50万元 | D. | 55万元 |
18.从某高中女学生中选取10名学生,根据其身高(cm)、体重(kg)数据,得到体重关于身高的回归方程$\widehat{y}$=0.85x-85,用来刻画回归效果的相关指数R2=0.6,则下列说法正确的是( )
| A. | 这些女学生的体重和身高具有非线性相关关系 | |
| B. | 这些女学生的体重差异有60%是由身高引起的 | |
| C. | 身高为170cm的学生体重一定为59.5kg | |
| D. | 这些女学生的身高每增加0.85cm,其体重约增加1kg |
8.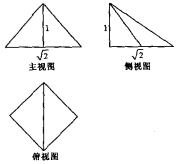 刘徽的《九章算术注》中有这样的记载:“邪解立方有两堑堵,邪解堑堵,其一为阳马,一为鳖臑,阳马居二,鳖臑居一,不易之率也.”意思是说:把一块立方体沿斜线分成相同的两块,这两块叫做堑堵,再把一块堑堵沿斜线分成两块,大的叫阳马,小的叫鳖臑,两者体积比为2:1,这个比率是不变的,如图是一个阳马的三视图,则其表面积为( )
刘徽的《九章算术注》中有这样的记载:“邪解立方有两堑堵,邪解堑堵,其一为阳马,一为鳖臑,阳马居二,鳖臑居一,不易之率也.”意思是说:把一块立方体沿斜线分成相同的两块,这两块叫做堑堵,再把一块堑堵沿斜线分成两块,大的叫阳马,小的叫鳖臑,两者体积比为2:1,这个比率是不变的,如图是一个阳马的三视图,则其表面积为( )
 刘徽的《九章算术注》中有这样的记载:“邪解立方有两堑堵,邪解堑堵,其一为阳马,一为鳖臑,阳马居二,鳖臑居一,不易之率也.”意思是说:把一块立方体沿斜线分成相同的两块,这两块叫做堑堵,再把一块堑堵沿斜线分成两块,大的叫阳马,小的叫鳖臑,两者体积比为2:1,这个比率是不变的,如图是一个阳马的三视图,则其表面积为( )
刘徽的《九章算术注》中有这样的记载:“邪解立方有两堑堵,邪解堑堵,其一为阳马,一为鳖臑,阳马居二,鳖臑居一,不易之率也.”意思是说:把一块立方体沿斜线分成相同的两块,这两块叫做堑堵,再把一块堑堵沿斜线分成两块,大的叫阳马,小的叫鳖臑,两者体积比为2:1,这个比率是不变的,如图是一个阳马的三视图,则其表面积为( )| A. | 2 | B. | 2+$\sqrt{2}$ | C. | 3+$\sqrt{3}$ | D. | 3+$\sqrt{2}$ |
15.已知全集U={2,3,4,5,6,7},集合A={4,5,7},B={4,6},则A∩(∁UB)=( )
| A. | {5} | B. | {2} | C. | {2,5} | D. | {5,7} |