题目内容
16.已知函数f(x)=lnx-2ax(其中a∈R).(Ⅰ)当a=1时,求函数f(x)的图象在x=1处的切线方程;
(Ⅱ)若f(x)≤1恒成立,求a的取值范围;
(Ⅲ)设g(x)=f(x)+$\frac{1}{2}$x2,且函数g(x)有极大值点x0,求证:x0f(x0)+1+ax02>0.
分析 (Ⅰ)当a=1时,${f}^{'}(x)=\frac{1}{x}$-2,由此利用导数的几何意义能求出函数f(x)的图象在x=1处的切线方程.
(Ⅱ)由不等式f(x)≤1,得2a≥$\frac{lnx-1}{x}$恒成立,令φ(x)=$\frac{lnx-1}{x}$(x>0),则φ′(x)=$\frac{2-lnx}{{x}^{2}}$,由此利用导数性质能求出实数a的取值范围.
(Ⅲ)由g(x)=f(x)+$\frac{1}{2}$x2=$\frac{1}{2}{x}^{2}-2ax+lnx$,得${g}^{'}(x)=x+\frac{1}{x}-2a=\frac{{x}^{2}-2ax+1}{x}$,分类讨论求出a=$\frac{{{x}_{0}}^{2}+1}{2{x}_{0}}$,由x0f(x0)+1+ax02=-$\frac{{{x}_{0}}^{3}}{2}-\frac{{x}_{0}}{2}+{x}_{0}ln{x}_{0}$+1,令h(x)=-$\frac{{x}^{3}}{2}-\frac{x}{2}+xlnx+1$,x∈(0,1),则${h}^{'}(x)=-\frac{3{x}^{2}}{2}+\frac{1}{2}+lnx$,利用构造法推导出h′(x)<0,由此能证明x0f(x0)+1+ax02>0.
解答 解:(Ⅰ)当a=1时,f(x)=lnx-2x,则${f}^{'}(x)=\frac{1}{x}$-2,x>0,
∴f(1)=-2,f′(1)=-1,
∴函数f(x)的图象在x=1处的切线方程为y-(-2)=-(x-1),即x+y+1=0.
(Ⅱ)不等式f(x)≤1,即lnx-2ax≤1,∴2ax≥lnx-1,
∵x>0,∴2a≥$\frac{lnx-1}{x}$恒成立,
令φ(x)=$\frac{lnx-1}{x}$(x>0),则φ′(x)=$\frac{2-lnx}{{x}^{2}}$,
当0<x<e2时,φ′(x)>0,φ(x)单调递增,当x>e2时,φ′(x)<0,φ(x)单调递减,
∴当x=e2时,φ(x)取得极大值,也为最大值,故φ(x)max=φ(e2)=$\frac{1}{{e}^{2}}$,
由2a≥$\frac{1}{{e}^{2}}$,得a≥$\frac{1}{2{e}^{2}}$,∴实数a的取值范围是[$\frac{1}{2{e}^{2}}$,+∞).
(Ⅲ)证明:由g(x)=f(x)+$\frac{1}{2}$x2=$\frac{1}{2}{x}^{2}-2ax+lnx$,得${g}^{'}(x)=x+\frac{1}{x}-2a=\frac{{x}^{2}-2ax+1}{x}$,
①当-1≤a≤1时,g(x)单调递增无极值点,不符合题意;
②当a>1或a<-1时,令g′(x)=0,设x2-2ax+1=0的两根为x0和x′,
∵x0为函数g(x)的极大值点,∴0<x0<x′,
由${x}_{0}{x}^{'}$=1,${x}_{0}+{x}^{'}=2a>0$,知a>1,0<x0<1,
又由g′(x0)=${x}_{0}+\frac{1}{{x}_{0}}-2a$=0,得a=$\frac{{{x}_{0}}^{2}+1}{2{x}_{0}}$,
∵${x}_{0}f({x}_{0})+1+a{{x}_{0}}^{2}={x}_{0}ln{x}_{0}-\frac{{{x}_{0}}^{2}+{x}_{0}}{2}+1$=-$\frac{{{x}_{0}}^{3}}{2}-\frac{{x}_{0}}{2}+{x}_{0}ln{x}_{0}$+1,0<x0<1,
令h(x)=-$\frac{{x}^{3}}{2}-\frac{x}{2}+xlnx+1$,x∈(0,1),则${h}^{'}(x)=-\frac{3{x}^{2}}{2}+\frac{1}{2}+lnx$,
令$μ(x)=-\frac{3{x}^{2}}{2}+\frac{1}{2}+lnx$,x∈(0,1),则${μ}^{'}(x)=-3x+\frac{1}{x}=\frac{1-3{x}^{2}}{x}$,
当$0<x<\frac{\sqrt{3}}{3}$时,μ′(x)>0,当$\frac{\sqrt{3}}{3}<x<1$时,μ′(x)<0,
∴μ(x)max=μ($\frac{\sqrt{3}}{3}$)=ln$\frac{\sqrt{3}}{3}$<0,∴h′(x)<0,
∴h(x)在(0,1)上单调递减,∴h(x)>h(1)=0,
∴x0f(x0)+1+ax02>0.
点评 本题考查了利用导数研究函数的单调性极值与最值、切线方程,考查了恒成立问题的等价转化方法,考查了推理论证能力与计算求解能力,属于难题.

| A. | xy≠10是x≠5或y≠2的充分不必要条件 | |
| B. | 若命题p:?x∈R,x2+x+1≠0,则¬p:?x∈R,x2+x+1=0 | |
| C. | 已知随机变量X~N(2,σ2),且P(X≤4)=0.84,则P(X≤0)=0.16 | |
| D. | 相关指数R2越接近1,表示残差平方和越大. |
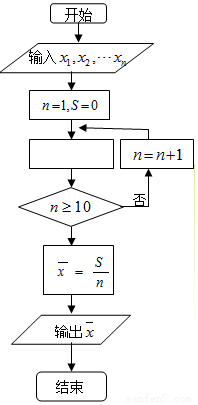 如图是求样本x1、x2、…x10平均数$\overline{x}$的程序框图,图中空白框中应填入的内容为( )
如图是求样本x1、x2、…x10平均数$\overline{x}$的程序框图,图中空白框中应填入的内容为( )| A. | S=S+xn | B. | S=S+$\frac{{x}_{n}}{n}$ | C. | S=S+n | D. | S=S+$\frac{{x}_{n}}{10}$ |
| 甲产品所需工时 | 乙产品所需工时 | |
| A设备 | 2 | 3 |
| B设备 | 4 | 1 |
| A. | 40万元 | B. | 45万元 | C. | 50万元 | D. | 55万元 |

| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
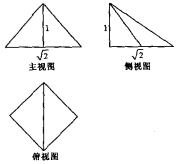 刘徽的《九章算术注》中有这样的记载:“邪解立方有两堑堵,邪解堑堵,其一为阳马,一为鳖臑,阳马居二,鳖臑居一,不易之率也.”意思是说:把一块立方体沿斜线分成相同的两块,这两块叫做堑堵,再把一块堑堵沿斜线分成两块,大的叫阳马,小的叫鳖臑,两者体积比为2:1,这个比率是不变的,如图是一个阳马的三视图,则其表面积为( )
刘徽的《九章算术注》中有这样的记载:“邪解立方有两堑堵,邪解堑堵,其一为阳马,一为鳖臑,阳马居二,鳖臑居一,不易之率也.”意思是说:把一块立方体沿斜线分成相同的两块,这两块叫做堑堵,再把一块堑堵沿斜线分成两块,大的叫阳马,小的叫鳖臑,两者体积比为2:1,这个比率是不变的,如图是一个阳马的三视图,则其表面积为( )| A. | 2 | B. | 2+$\sqrt{2}$ | C. | 3+$\sqrt{3}$ | D. | 3+$\sqrt{2}$ |