题目内容
20.已知$\overrightarrow m$=(cos$\frac{x}{2}$,sin$\frac{x}{2}$),$\overrightarrow n$=(-$\sqrt{3}$,1),x∈R,则|$\overrightarrow m$-$\overrightarrow n$|的最大值是3.分析 根据向量的坐标运算和向量的模以及三角函数的化简,以及正弦函数的性质即可求出.
解答 解:∵$\overrightarrow m$=(cos$\frac{x}{2}$,sin$\frac{x}{2}$),$\overrightarrow n$=(-$\sqrt{3}$,1),
∴$\overrightarrow{m}$-$\overrightarrow{n}$=(cos$\frac{x}{2}$+$\sqrt{3}$,sin$\frac{x}{2}$-1),
∴|$\overrightarrow{m}$-$\overrightarrow{n}$|2=(cos$\frac{x}{2}$+$\sqrt{3}$)2+(sin$\frac{x}{2}$-1)2=5+2($\sqrt{3}$cos$\frac{x}{2}$-sin$\frac{x}{2}$)=5+4sin($\frac{π}{3}$-$\frac{x}{2}$)≤5+4=9,
∴|$\overrightarrow m$-$\overrightarrow n$|的最大值是3,
故答案为:3
点评 本题考查了向量的坐标运算和向量的模以及三角函数的化简,以及正弦函数的性质,属于基础题.

练习册系列答案
相关题目
11.某工厂拟生产甲、乙两种实销产品.已知每件甲产品的利润为0.4万元,每件乙产品的利润为0.3万元,两种产品都需要在A,B两种设备上加工,且加工一件甲、乙产品在A,B设备上所需工时(单位:h)分别如表所示.
若A设备每月的工时限额为400h,B设备每月的工时限额为300h,则该厂每月生产甲、乙两种产品可获得的最大利润为( )
| 甲产品所需工时 | 乙产品所需工时 | |
| A设备 | 2 | 3 |
| B设备 | 4 | 1 |
| A. | 40万元 | B. | 45万元 | C. | 50万元 | D. | 55万元 |
8.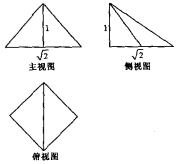 刘徽的《九章算术注》中有这样的记载:“邪解立方有两堑堵,邪解堑堵,其一为阳马,一为鳖臑,阳马居二,鳖臑居一,不易之率也.”意思是说:把一块立方体沿斜线分成相同的两块,这两块叫做堑堵,再把一块堑堵沿斜线分成两块,大的叫阳马,小的叫鳖臑,两者体积比为2:1,这个比率是不变的,如图是一个阳马的三视图,则其表面积为( )
刘徽的《九章算术注》中有这样的记载:“邪解立方有两堑堵,邪解堑堵,其一为阳马,一为鳖臑,阳马居二,鳖臑居一,不易之率也.”意思是说:把一块立方体沿斜线分成相同的两块,这两块叫做堑堵,再把一块堑堵沿斜线分成两块,大的叫阳马,小的叫鳖臑,两者体积比为2:1,这个比率是不变的,如图是一个阳马的三视图,则其表面积为( )
 刘徽的《九章算术注》中有这样的记载:“邪解立方有两堑堵,邪解堑堵,其一为阳马,一为鳖臑,阳马居二,鳖臑居一,不易之率也.”意思是说:把一块立方体沿斜线分成相同的两块,这两块叫做堑堵,再把一块堑堵沿斜线分成两块,大的叫阳马,小的叫鳖臑,两者体积比为2:1,这个比率是不变的,如图是一个阳马的三视图,则其表面积为( )
刘徽的《九章算术注》中有这样的记载:“邪解立方有两堑堵,邪解堑堵,其一为阳马,一为鳖臑,阳马居二,鳖臑居一,不易之率也.”意思是说:把一块立方体沿斜线分成相同的两块,这两块叫做堑堵,再把一块堑堵沿斜线分成两块,大的叫阳马,小的叫鳖臑,两者体积比为2:1,这个比率是不变的,如图是一个阳马的三视图,则其表面积为( )| A. | 2 | B. | 2+$\sqrt{2}$ | C. | 3+$\sqrt{3}$ | D. | 3+$\sqrt{2}$ |
15.已知全集U={2,3,4,5,6,7},集合A={4,5,7},B={4,6},则A∩(∁UB)=( )
| A. | {5} | B. | {2} | C. | {2,5} | D. | {5,7} |
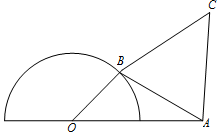 半圆O直径为2,OA=2,B为半圆上任意一点,C为半圆外异于A的点,以AB为边按顺时针方向作正△ABC,问B在何位置时,四边形OACB面积最大?
半圆O直径为2,OA=2,B为半圆上任意一点,C为半圆外异于A的点,以AB为边按顺时针方向作正△ABC,问B在何位置时,四边形OACB面积最大?