题目内容
11.对任意实数x,不等式3sinx-4cosx+c>0恒成立,则c的取值范围是c>5.分析 化3sinx-4cosx+c>0为c>-5sin(x-m),
利用-1≤sin(x-m)≤1求出c的取值范围.
解答 解:∵3sinx-4cosx+c>0恒成立,
∴3sinx-4cosx=5sin(x-m)>-c恒成立,
即c>-5sin(x-m)恒成立;
又∵-1≤sin(x-m)≤1,
∴-5sin(x-m)≤5;
∴c的取值范围是c>5.
故答案为:c>5.
点评 本题考查了三角函数不等式的恒成立问题,也考查了三角函数的有界性问题,是基础题.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
1.已知函数f(x)=ax-ln x,若f(x)>1在区间(1,+∞)内恒成立,则实数a的取值范围是( )
| A. | (-∞,1) | B. | (-∞,1] | C. | (1,+∞) | D. | [1,+∞) |
19.设m,n为两条不同的直线,α,β为两个不同的平面,给出下列命题:
①若m⊥α,m⊥β,则α∥β②若m∥α,m∥β,则α∥β③若m∥α,n∥α,则m∥n④若m⊥α.n⊥α,则m∥n
上述命题中,所有真命题的序号是( )
①若m⊥α,m⊥β,则α∥β②若m∥α,m∥β,则α∥β③若m∥α,n∥α,则m∥n④若m⊥α.n⊥α,则m∥n
上述命题中,所有真命题的序号是( )
| A. | ①④ | B. | ②③ | C. | ①③ | D. | ②④ |
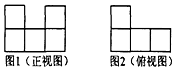 用若干个棱长为1cm的小正方体叠成一个几何体,图1为其正视图,图2为其俯视图,若这个几何体的体积为7cm3,则其侧视图为( )
用若干个棱长为1cm的小正方体叠成一个几何体,图1为其正视图,图2为其俯视图,若这个几何体的体积为7cm3,则其侧视图为( )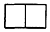


 正三棱柱ABC-A1B1C1底边长为2,E、F分别为BB1,AB的中点,设$\frac{A{A}_{1}}{AB}$=λ.
正三棱柱ABC-A1B1C1底边长为2,E、F分别为BB1,AB的中点,设$\frac{A{A}_{1}}{AB}$=λ.