题目内容
以双曲线的一条焦半径为直径的圆与以实轴为直径的圆的位置关系为( )
| A、相交 | B、内切 |
| C、外切 | D、内切或外切 |
考点:双曲线的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:利用双曲线的定义,通过圆心距判断出当点P分别在左、右两支时,两圆相内切、外切.
解答:
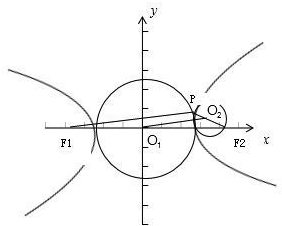 解:设以实轴|F1F2|为直径的圆的圆心为O1,其半径r1=a,
解:设以实轴|F1F2|为直径的圆的圆心为O1,其半径r1=a,
线段PF2为直径的圆的圆心为O2,其半径为r2=
,
当P在双曲线左支上时,|O1O2|=
,
∵r|O1O2|-r2=
-
=a=r1,
∴两圆内切.
当P在双曲线右支上时,
|O1O2|=
,
∵|O1O2|-r2=
-
=a=r1,
∴r1+r2=|O1O2|
∴两圆外切.
故选:D.
 解:设以实轴|F1F2|为直径的圆的圆心为O1,其半径r1=a,
解:设以实轴|F1F2|为直径的圆的圆心为O1,其半径r1=a,线段PF2为直径的圆的圆心为O2,其半径为r2=
| |PF2| |
| 2 |
当P在双曲线左支上时,|O1O2|=
| |PF1| |
| 2 |
∵r|O1O2|-r2=
| |PF2| |
| 2 |
| |PF1| |
| 2 |
∴两圆内切.
当P在双曲线右支上时,
|O1O2|=
| |PF1| |
| 2 |
∵|O1O2|-r2=
| |PF1| |
| 2 |
| |PF2| |
| 2 |
∴r1+r2=|O1O2|
∴两圆外切.
故选:D.
点评:本题考查直线和双曲线的位置关系,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,易错点是容易只考虑P点在一个分支上而导致丢解,是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
已知全集U=R,A={x|x≤-2},B={x|x≥1},则集合∁U(A∪B)=( )
| A、{x|-2<x<1} |
| B、{x|x≤1} |
| C、{x|-2≤x≤1} |
| D、{x|x≥-2} |
若方程
-
=1表示双曲线,则λ的取值范围是( )
| x2 |
| 2+λ |
| y2 |
| 1+λ |
| A、λ>-1 |
| B、λ<-2 |
| C、-2<λ<-1 |
| D、λ>-1或λ<-2 |
函数y=(a2-3a+3)•ax(x∈N+)为正整数指数函数,则a等于( )
| A、1 | B、2 |
| C、1或2 | D、以上都不对 |
若某程序框图如图所示,则输出的n的值是( )


| A、5 | B、6 | C、7 | D、8 |
如果A(2,2),B(a,0),C(0,4)三点共线,则a的值是( )
| A、-3 | B、3 | C、4 | D、-4 |
已知F是双曲线
-
=1的右焦点,点P在双曲线上,点Q在圆(x-8)2+(y-2)2=1上,则|PF|+|PQ|的最小值为( )
| x2 |
| 5 |
| y2 |
| 4 |
A、3
| ||
B、
| ||
C、5
| ||
D、7
|