题目内容
20.(1)函数y=3cos(2x-$\frac{π}{3}$),x∈R在什么区间上是减函数?(2)函数y=sin(-3x+$\frac{π}{4}$),x∈R在什么区间上是增函数?
分析 根据三角函数的单调性列出不等式解出.
解答 解:(1)令2kπ≤2x-$\frac{π}{3}$≤π+2kπ,解得$\frac{π}{6}+kπ$≤x≤$\frac{2π}{3}+kπ$.
∴y=3cos(2x-$\frac{π}{3}$)在区间[$\frac{π}{6}+kπ$,$\frac{2π}{3}+kπ$]上是减函数;
(2)y=-sin(3x-$\frac{π}{4}$),
令$\frac{π}{2}+2kπ≤$3x-$\frac{π}{4}$≤$\frac{3π}{2}+2kπ$,解得$\frac{π}{4}$+$\frac{2kπ}{3}$≤x≤$\frac{7π}{12}$+$\frac{2kπ}{3}$.
∴函数y=sin(-3x+$\frac{π}{4}$)在区间[$\frac{π}{4}$+$\frac{2kπ}{3}$,$\frac{7π}{12}$+$\frac{2kπ}{3}$]上是增函数.
点评 本题考查了三角函数的单调性,属于中档题.

练习册系列答案
相关题目
12.已知等比数列{an}的前n项和为Sn,S2n=3(a1+a3+…+a2n-1),a2a3a4=8,则a7=( )
| A. | 32 | B. | 64 | C. | 54 | D. | 162 |
7.已知变量x与y线性相关,且由观测数据算得样本平均数分别为$\overline{x}$=4,$\overline{y}$=3,则由该观测数据算得的线性回归方程不可能是( )
| A. | $\widehat{y}$=0.2x+2.2 | B. | $\widehat{y}$=0.3x+1.8 | C. | $\widehat{y}$=0.4x+1.4 | D. | $\widehat{y}$=0.5x+1.2 |
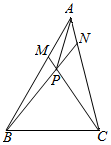 如图所示,在三角形ABC中,AM:AB=1:3,AN:AC=1:4,BN与CM相交于P,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,试用$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{AP}$.
如图所示,在三角形ABC中,AM:AB=1:3,AN:AC=1:4,BN与CM相交于P,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,试用$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{AP}$.