题目内容
19.已知数列{an}的前n项和是Sn,且Sn+$\frac{1}{2}$an=1(n∈N*).(1)求数列{an}的通项公式;
(2)设bn=$lo{g}_{\frac{1}{3}}$(1-Sn+1)(n∈N*),求数列{$\frac{1}{{b}_{n}{b}_{n+1}}$}的前n项和Tn.
分析 (1)当n=1时可求得a1=$\frac{2}{3}$,当n≥2时,化简可得an=$\frac{1}{3}$an-1,从而求通项公式;
(2)化简bn=$lo{g}_{\frac{1}{3}}$(1-Sn+1)=n+1,从而化简$\frac{1}{{b}_{n}{b}_{n+1}}$=$\frac{1}{1+n}$-$\frac{1}{n+2}$,从而利用裂项求和法求其和.
解答 解:(1)当n=1时,S1+$\frac{1}{2}$a1=1,
故a1=$\frac{2}{3}$;
当n≥2时,Sn+$\frac{1}{2}$an=1,Sn-1+$\frac{1}{2}$an-1=1,
故an+$\frac{1}{2}$an-$\frac{1}{2}$an-1=0,
故an=$\frac{1}{3}$an-1,
故数列{an}是以$\frac{2}{3}$为首项,$\frac{1}{3}$为公比的等比数列,
故an=$\frac{2}{3}$•($\frac{1}{3}$)n-1=$\frac{2}{{3}^{n}}$;
(2)由(1)知,1-Sn+1=$\frac{1}{2}$•an+1=$\frac{1}{{3}^{n+1}}$,
故bn=$lo{g}_{\frac{1}{3}}$(1-Sn+1)=n+1,
故$\frac{1}{{b}_{n}{b}_{n+1}}$=$\frac{1}{(n+1)(n+2)}$=$\frac{1}{1+n}$-$\frac{1}{n+2}$,
故Tn=($\frac{1}{2}$-$\frac{1}{3}$)+($\frac{1}{3}$-$\frac{1}{4}$)+…+($\frac{1}{1+n}$-$\frac{1}{n+2}$)
=$\frac{1}{2}$-$\frac{1}{n+2}$=$\frac{n}{2(n+2)}$.
点评 本题考查了分类讨论的思想应用及等比数列的性质应用,同时考查了对数运算的应用.

| A. | $\widehat{y}$=0.2x+2.2 | B. | $\widehat{y}$=0.3x+1.8 | C. | $\widehat{y}$=0.4x+1.4 | D. | $\widehat{y}$=0.5x+1.2 |
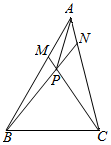 如图所示,在三角形ABC中,AM:AB=1:3,AN:AC=1:4,BN与CM相交于P,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,试用$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{AP}$.
如图所示,在三角形ABC中,AM:AB=1:3,AN:AC=1:4,BN与CM相交于P,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,试用$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{AP}$.